Let ε1andε2 be the angles made by →Aand−→A with the positive X-axis. Show that tanε1=tanε2. Thus giving tanε does not uniquely determine of →A.
To solve the problem, we need to show that the tangent of the angles made by the vector →A and −→A with the positive X-axis are equal. Let's denote the angle made by →A with the positive X-axis as ϵ1 and the angle made by −→A with the positive X-axis as ϵ2.
Step 1: Understand the Angles
The angle ϵ1 is the angle that the vector →A makes with the positive X-axis. The vector −→A is in the opposite direction of →A, which means that the angle ϵ2 made by −→A with the positive X-axis can be expressed in terms of ϵ1.
Step 2: Relate the Angles
Since −→A is in the opposite direction of →A, we can express ϵ2 in terms of ϵ1:
ϵ2=ϵ1+180∘
Step 3: Apply the Tangent Function
Now, we can apply the tangent function to both sides of the equation:
tan(ϵ2)=tan(ϵ1+180∘)
Step 4: Use the Tangent Addition Formula
Using the property of the tangent function, we know that:
tan(θ+180∘)=tan(θ)
Thus, we can write:
tan(ϵ2)=tan(ϵ1)
Conclusion
From the above steps, we have shown that:
tan(ϵ1)=tan(ϵ2)
This indicates that the tangent of the angle does not uniquely determine the vector →A because both →A and −→A yield the same tangent value.
The angle ϵ1 is the angle that the vector →A makes with the positive X-axis. The vector −→A is in the opposite direction of →A, which means that the angle ϵ2 made by −→A with the positive X-axis can be expressed in terms of ϵ1.
Since −→A is in the opposite direction of →A, we can express ϵ2 in terms of ϵ1:
ϵ2=ϵ1+180∘
Now, we can apply the tangent function to both sides of the equation:
tan(ϵ2)=tan(ϵ1+180∘)
Using the property of the tangent function, we know that:
tan(θ+180∘)=tan(θ)
Thus, we can write:
tan(ϵ2)=tan(ϵ1)
From the above steps, we have shown that:
tan(ϵ1)=tan(ϵ2)
This indicates that the tangent of the angle does not uniquely determine the vector →A because both →A and −→A yield the same tangent value.
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises
34 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer
17 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
Similar Questions
The angle made by the vector →A=2ˆi+3ˆj with Y-axis is
View SolutionThe angle made by the vector →A=ˆi+ˆj with x-axis is
View SolutionThe angle that the vector →A=2ˆi+3ˆj makes with y-axis is :
View SolutionDetermine current through batteries ε1 and ε2
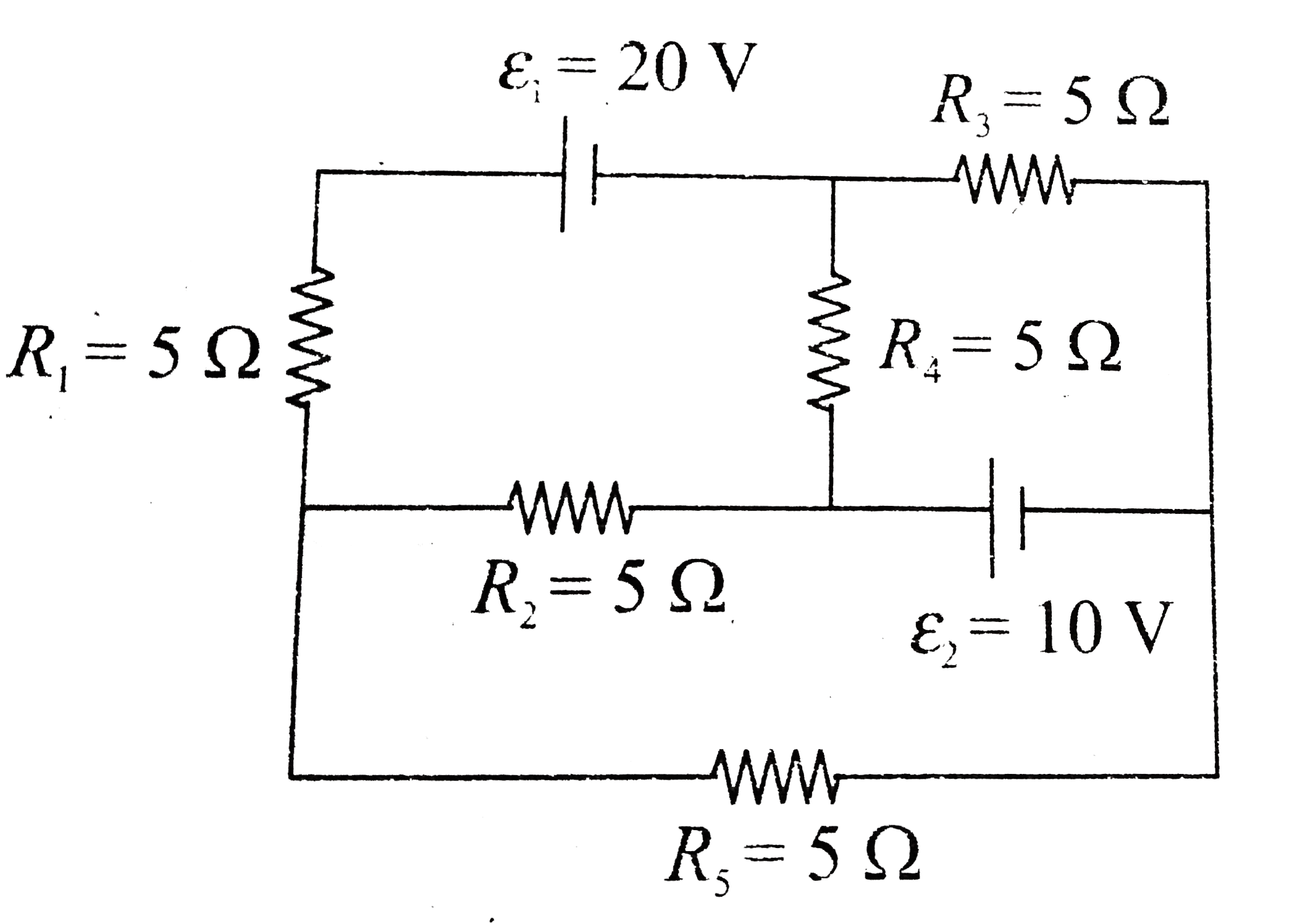
View SolutionFind the angle between two →a and →b with magnitudes 1 and 2 respectively and when →a.→b=1.
View SolutionFind the angle between two vectors →aand→b with magnitudes 1 and 2 respectively and satisfying →a.→b.=1
View SolutionLet →a be a vector in the xy - plane making an angle of 60∘ with the positive x - axis and ∣∣→a−ˆi∣∣ is the geometric mean of |→a| and ∣∣→a−2ˆi∣∣, then the value of |→a| is equal to
View SolutionLet →a and →b are unit vectors inclined at an angle α to each other , if ∣∣→a+→b∣∣<1 then
View SolutionIf →a and →b are unit vectors and θ is the angle between them then show that
∣∣→a−→b∣∣=2sin.θ2
View SolutionIf θ is the angle between the unit vectors →aand→b, then prove that
i. cos(θ2)=12∣∣→a+→b∣∣
ii.sin(θ2)=12∣∣→a−→b∣∣
View Solution
