Match the following columns.
∣∣
∣
∣
∣
∣
∣
∣
∣∣Column IColumn II(A)d v/dt(p)Acceleration(B)d|v|/dt(q)Magnitude of acceleration(C)drdt(r)Velocity(D)∣∣drdt∣∣(s)Magnitude of velocity(t)Rate of change of speed∣∣
∣
∣
∣
∣
∣
∣
∣∣
The correct Answer is:A, B, C, D
d|v|dt is rate of change of speed of the particle.
d|r|dt in the rate by which distance of particle from the origin is changing.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)
19 Videos
- MOTIONBOOK - DC PANDEYCHAPTER - MOTIONEXERCISE - Medical entrances gallery
19 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
Similar Questions
Match the following :
Column IColumn II(a)Penicillin(p)Bacteriostatic(b)Chloramphenicol(q)Antibiotic(c)Aspirin(r)Bacteriocidal(d)Ibuprofen(s)Analgesic(t)Antipyretic
View SolutionMatch the following
Column-IColumn-II(A)Derived unit(p)Height(B)Fundamental unit(q)Thickness(C)Derived quantity(r)Area(D)Fundamental quantity(s)Newton(t)Kilogram
View Solution
Knowledge Check
Match the columns
Column IColumn IIaBicuspid valvepBrainbNephronqLivercAlveolirHeartdCerebrumsKidneytLungsAa−s,b−r,c−p,d−tBa−r,b−t,c−s,d−pCa−r,b−s,c−t,d−pDa−s,b−q,c−p,d−t
For the velocity -time graph shown in figure, in a time interval from t=0 to t=6s, match the following:
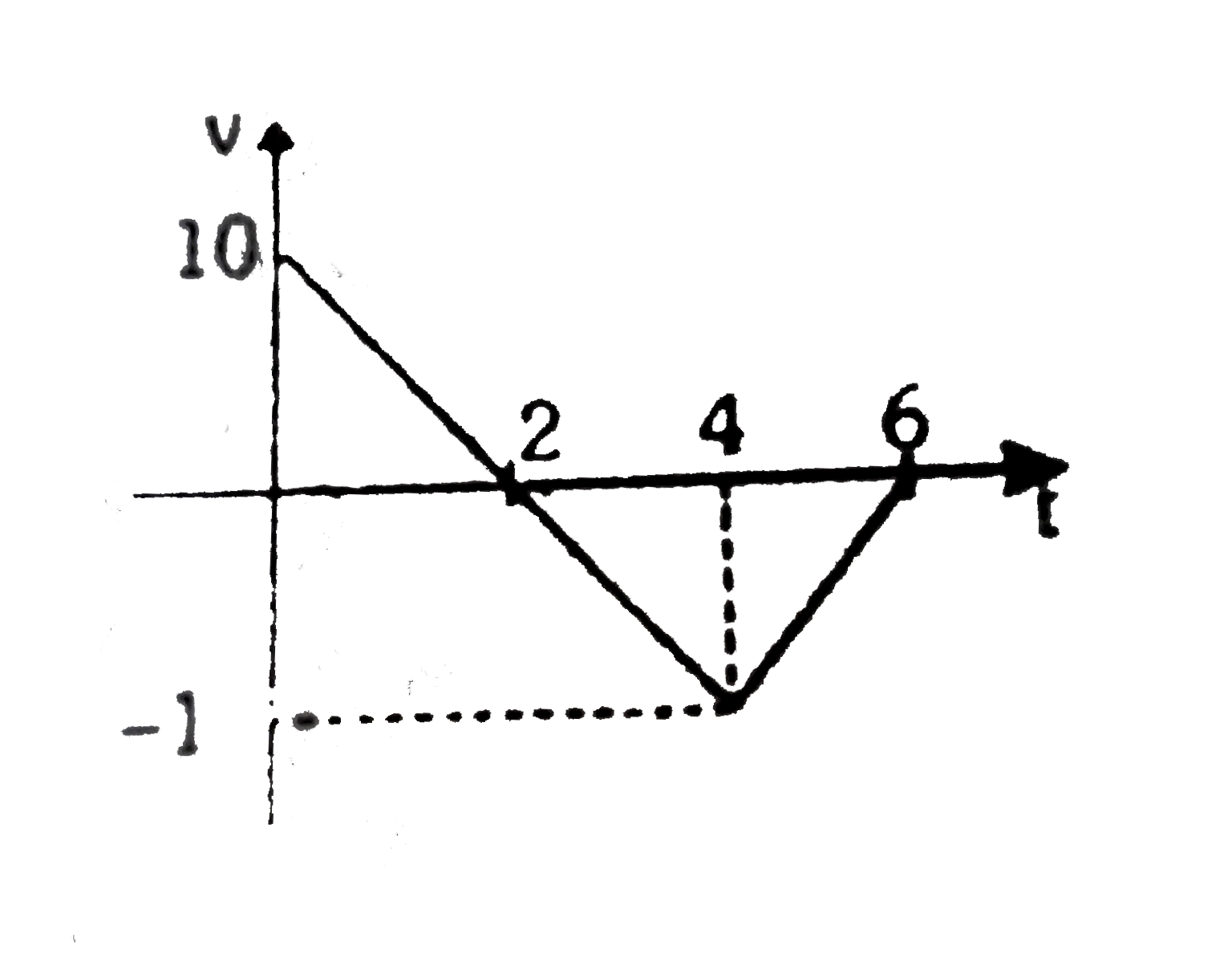
Column IColumn II(A)Change in velocity(p)−5/3SIunit(B)Average acceleration(q)−20SIunit(C)Total displacement(r)−10SIunit(D)Acceleration ay t=3s(s)−5SIunit
View SolutionColumn IColumn II(a)Work(p)Metre(b)Force(q)Joule(c)Displacement(r)Metre/second2(d)Acceleration due to gravity(s)Newton
View SolutionMatch Column-I with Column-II
Column-IColumn-II(A)XeF2(p)Square pyramidal(B)PCl5(q)linear shape(C)XeOF4(r)sp3dhybridization(D)XeF4(s)sp3d2
View SolutionThe equation of one dimensional motion of the particle is described in column I. At t=0, particle is at origin and at rest. Match the column I with the statement in Column II.
Column IColumn II(A)x=(3t2+2)m(p)Velocity of particle at t=1s is 8m/s(B)v=8tm/s(q)Particle moves with uniform acceleration(C)a=16t(r)Particle moves with variable acceleration(D)v=6t−3t2(s)Particle will change its direction some time
View SolutionMatch the column
Column IColumn II(A). Sucrose(P). α−D Glucose(B). Maltose(Q). β−Fructose(C). Lactose(R). β−D−Glucose(S). β−D−Galactose
View SolutionMatch the Column-I with Column-II :
Column-IColumn-II(a)Rate of reaction(p)May be fractional(b)Rate of constant(q)Whole number(c)Order of reaction(r)Indepdent of temperature(d)Molecularity of raction(s)Increase with temperature
View SolutionHere each question contains statements given in two columns which have to be matched. Statement in Column I are labelled as A,B, C are D whereas statements in column II are labelled as p,q,r and s. the answers to these questions are to be appropriately bubbled as illustrated in the following example. If the correct matches are A-p, A-s, B-q, B-r, C-p, C-q and D-p then the correctly labelled 4×4 matrix look like.

ColumnIColumnII(A)Molality(p)Elevation on boiling point(B)Molarity(q)Volume of solution(C)Normality(r)Wt of solvent(D)Mole fraction(s)Moles of solute
View Solution
