Moment of inertia of a straight wire about an axis perpendicular to the wire passing through one of its end is I.
Now the same wire is bent into a ring of two turns , then the moment of inertia would be
(π23)l
(π212)l
(316π2)l
(34π2)l
The correct Answer is:C
To find the moment of inertia of a straight wire bent into a ring of two turns, we can follow these steps:
Step 1: Understand the Moment of Inertia of the Straight Wire
The moment of inertia I of a straight wire about an axis perpendicular to the wire passing through one of its ends is given as:
I=ML23
where M is the mass of the wire and L is its length.
Step 2: Relate Length of the Wire to the Ring
When the wire is bent into a ring of two turns, the total length of the wire remains the same. The circumference of a single turn of the ring is 2πr, so for two turns, it becomes:
2×(2πr)=4πr
Setting this equal to the length of the wire L:
4πr=L
From this, we can solve for r:
r=L4π
Step 3: Calculate the Moment of Inertia of the Ring
The moment of inertia I′ of a ring about an axis passing through its center and perpendicular to its plane is given by:
I′=MR2
Substituting r from the previous step:
I′=M(L4π)2
This simplifies to:
I′=ML216π2
Step 4: Substitute for ML2
From the expression for the moment of inertia of the straight wire, we know:
ML2=3I
Substituting this into the equation for I′:
I′=3I16π2
Conclusion
Thus, the moment of inertia of the wire bent into a ring of two turns is:
I′=3I16π2
The moment of inertia I of a straight wire about an axis perpendicular to the wire passing through one of its ends is given as:
I=ML23
where M is the mass of the wire and L is its length.
When the wire is bent into a ring of two turns, the total length of the wire remains the same. The circumference of a single turn of the ring is 2πr, so for two turns, it becomes:
2×(2πr)=4πr
Setting this equal to the length of the wire L:
4πr=L
From this, we can solve for r:
r=L4π
The moment of inertia I′ of a ring about an axis passing through its center and perpendicular to its plane is given by:
I′=MR2
Substituting r from the previous step:
I′=M(L4π)2
This simplifies to:
I′=ML216π2
From the expression for the moment of inertia of the straight wire, we know:
ML2=3I
Substituting this into the equation for I′:
I′=3I16π2
Thus, the moment of inertia of the wire bent into a ring of two turns is:
I′=3I16π2
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
16 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
Moment of inertia of a straight wire about an axis perpendicular to the wire passing through one of its end is I.
This wire is now framed into a circle (a ring) of single turn. The moment of inertia of this ring about an axis passing through centre and perpendicular to its plane would be
View SolutionCalculate the moment of inertia of a rod of mass M, and length l about an axis perpendicular to it passing through one of its ends.
View SolutionCalculate the moment of inertia of a rod of mass 2 kg and length 5 m about an axis perpendicular to it and passing through one of its ends.
View SolutionThe moment of inertia of a uniform rod about a perpendicular axis passing through one end is I1. The same rod is bent into a ring and its moment of inertia about a diameter is I2. Then I1/I2 is
View SolutionThe moment of inertia of a straight thin rod of mass M and length l about an axis perpendicular to its length and passing through its one end, is
View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View SolutionThe moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through -
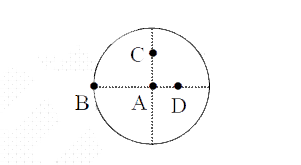
View SolutionFind the ratio of moment of inertia about axis perpendicular to rectangular plate passing through O & O
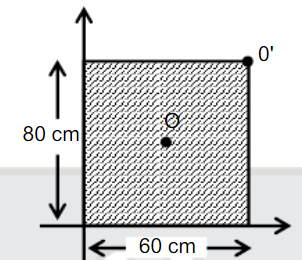
View SolutionFind the ratio of moment of inertia about axis perpendicular to rectangular plate passing through O & O

View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View Solution
