Monochramatic light is incident on the pLane interface AB between two media of refractive indices μ1 and μ2(μ2>μ1) at an angle of incidence theta as shown in figure. The angle theta is infinitesimally greater thannte critical angle for the two media so thast total internal reflection takes place. Now, if a transparent slab DEFG of uniform thickness and of refractive inde μ2 is introduced on theinterface (as shown in figure ) , show that for any value of μ2 all light will ultimately be reflected back into medium II.
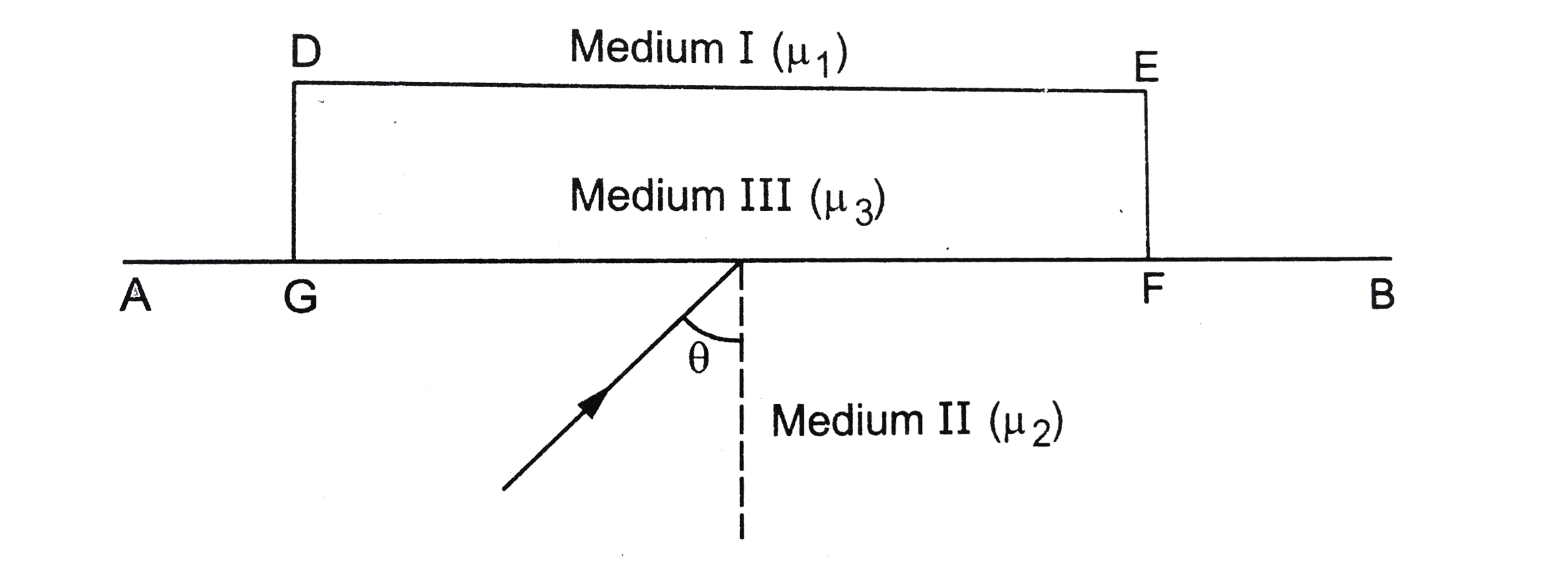
Given, θ is slightly greater than sin−1(μ1μ2)
When μ3<μ1
i.e. μ3<μ1<μ2
or μ3μ2<μ1μ2 or sin−1(μ3μ2)<sin−1(μ1μ2)
Hence, critical angle for III and II will be less than the critical angle for II and I. So, if TIR
is taking place between I and II, Then TIR will definitely take place between I and III.
When μ3>μ1 two cases may arise: Case1 μ1<μ3<μ2
In this case, there will be no TIR between II and III
but TIR will take place between III and I.
This is becuase
Ray of light first enters from II to III. i.e. from
denser to rarer.
∴i>θ
Applying Snell's law at P,
μ2sinθ=μ3sini or sini=(μ2μ3sinθ
Since, sinθ is slightly greater than μ1μ2.
∴sini is slightly greater than μ2μ3×μ1μ2 or μ1μ3
but μ1μ3 is nothing but sin(θC)I,III
∴sin(i) is slightly greater than sin(theta_C)_(I,III)<br>orTIRwillnowtakeplaceonIandIIIandtherayoflightwillberef≤ctedback.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V05_C31_S01_033_S01.pngwh=80%mx-autosty≤=background:white;><br>Case2mu_1ltmu_2ltmu_3<br>Thistimewhi≤mov∈gomIIandIII,rayoflightwill<br>bend→wards∥a∥l.Aga∈apply∈gS≠ll'slawatP,<br>mu_2 sin theta =mu_3 sini<br>sini=mu_2/mu_3 sin theta<br>Since,sin thetaisslightlygreaterthanmu_1/mu_2.<br>Therefore,sin iwillbeslightlythan(mu_2/mu_3xxmu_1/mu_2)or(mu_1/mu_3)<br>But,mu_1/mu_3issin (theta_C)_(I,III)<br>i.e.sinigtsin(theta_C)_(I,III)<br>sinigtsin(theta_C)_(I,III)<br>igt(theta_C)_(I,III)
Therefore, TIR will again take place between I and III and the ray light will be reflected back.

Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 10
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 11
3 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
What is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
View SolutionTwo refracting media are separated by a spherical interface as shown in the figure.

View SolutionA light ray is incident on a glass sphere of reflective index μ=√3 at an angle of incidence 60∘ as shown in Fig. Find the angles r, r′ e and the total deviation after two refractions.
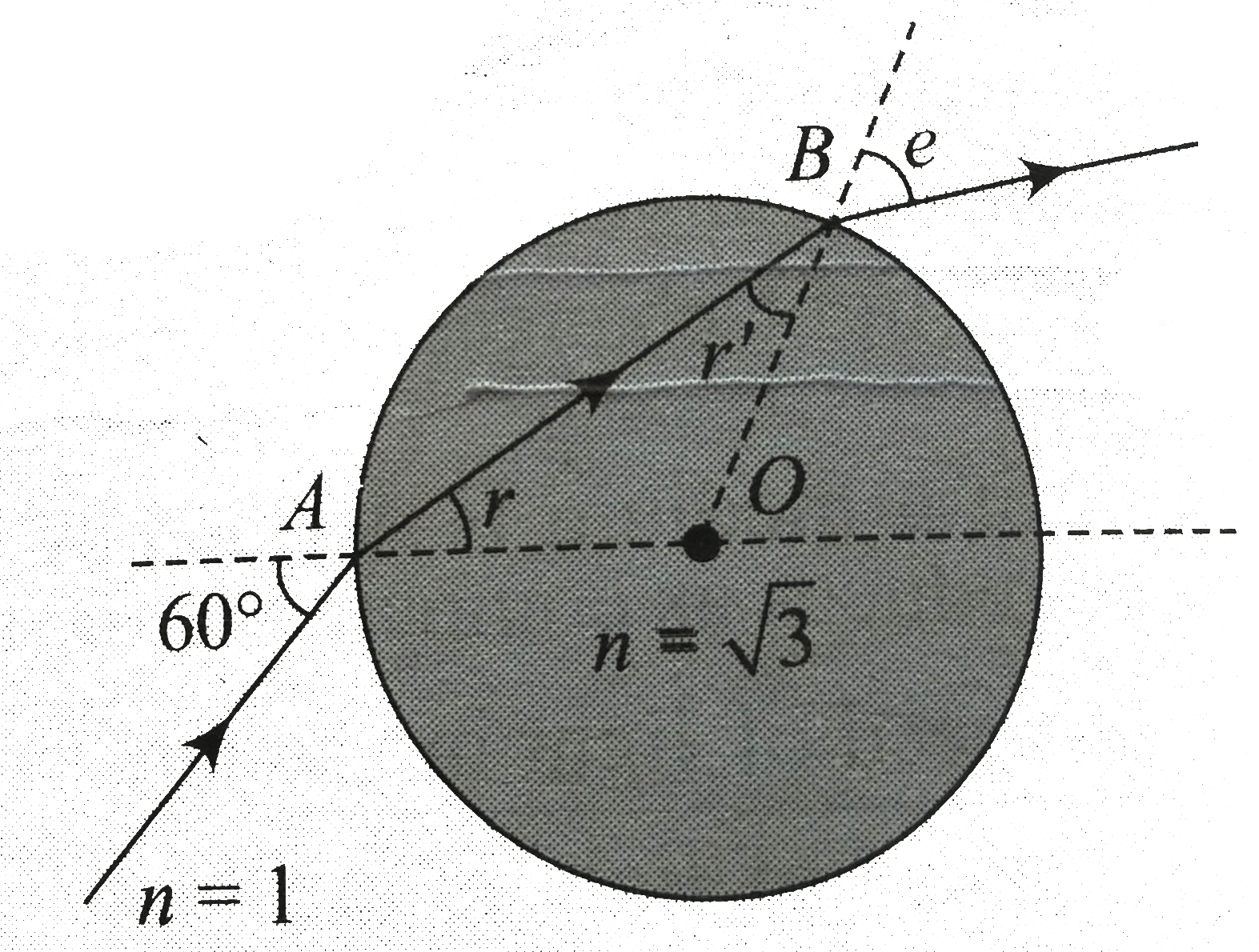
View SolutionFor total internal reflection to take place, the angle of incidence i and the refractive index μ of the medium must satisfy the inequality
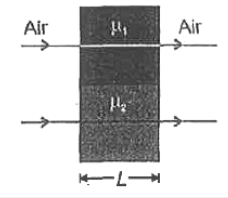
View SolutionTwo light rays initially in same phase travel through two media of equal length L having refraction index μ1andμ2(μ1>μ2) as shown in figure. If the wavelength of light rays in air is λ, the phase difference of the emerging rays is given by
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
View SolutionWhen a monochromatic light ray is incident on a medium of refracive indexμwith angle of incidence θ1,the angle of refraction is θr.if θi is changed slightly byΔθi,then the corresponding change in θrwill be-
View Solution
A ray is incident on interface of two media at critical angle as shown in the figure.
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View Solution
