O is the centre of an equilateral triangle ABC. →F1,→F2and→F3 are the three forces acting along the sides AB, BC and AC as shown in the figure. What should be the magnitude of →F3 so that the total torque about O is zero ?

F1+F22
F1−F2
2(F1+F2)
F1+F2
The correct Answer is:D
Let AO = BO = CO = r
The sum of the torques of →F1,→F2and→F3 about O
=→r×→F1+→r×→F2−→r×→F3=0
∴→r×→F1+→r×→F2=→r×→F3
From this we get F1+F2=F3.
Topper's Solved these Questions
Similar Questions
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
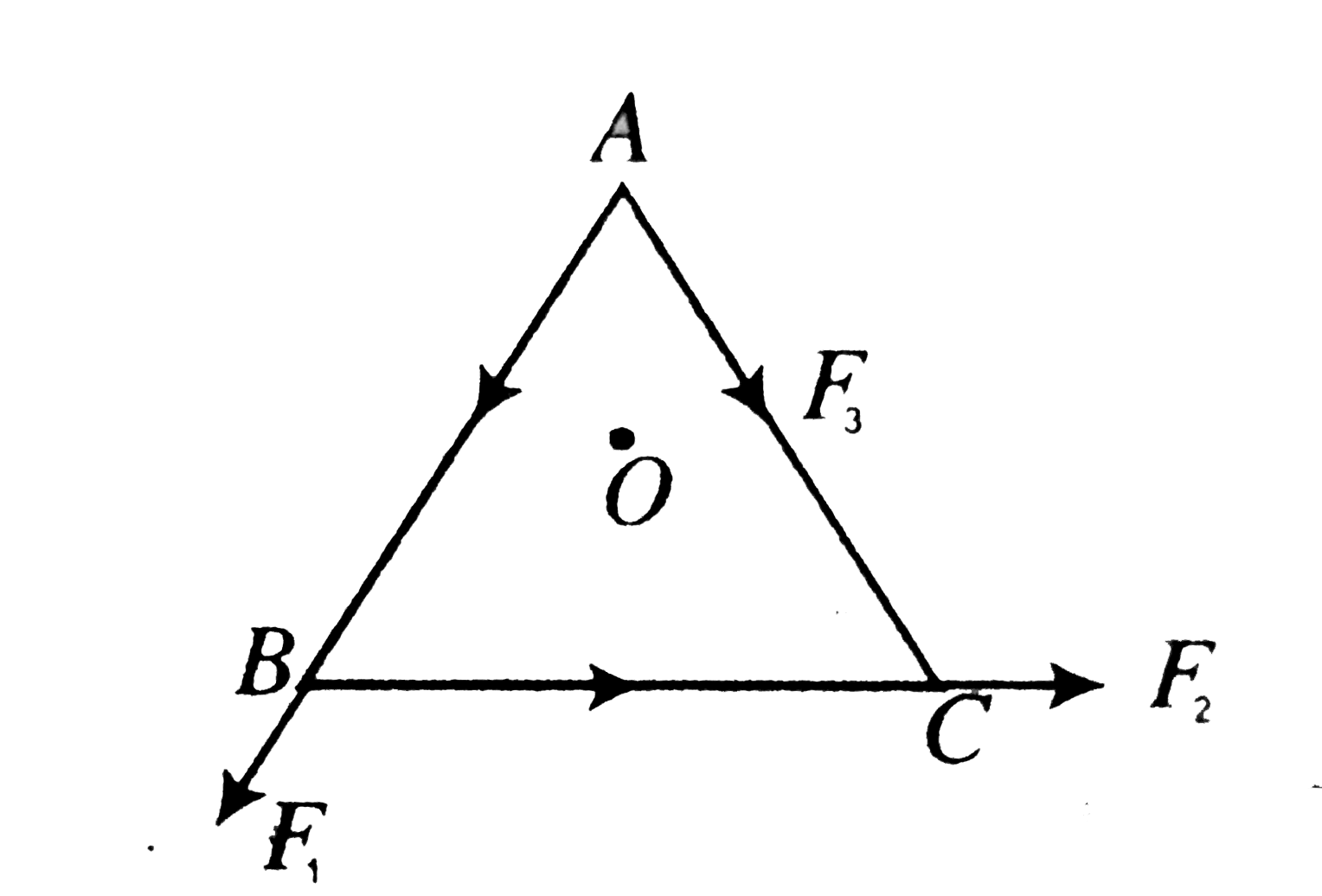 View Solution
View SolutionABC is an equilateral with O as its centre →F1,→F2 and →F3 represent three forces acting along the sides AB, BC and AC respectively. If the total torque about O is zero then the magnitude of →F3 is :
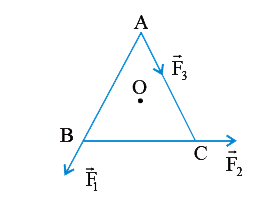 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are three forces acting along the sides AB, BC and AC as shown in the figure. What should be the magnitude of F3, so that the total torque about O is
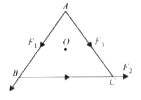 A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2)
A(F1+F2)B2(F1+F2)C(F1+F2)/2D(F1−F2) - Question 2 - Select One
O is the centre of an equilateral triangle ABC. F1,F2 and F3 are the three forces acting along the sides AB,BC and AC respectively. What should be the value of F3 so that the total torque about O is zero?
 A2(F1+F2)BF1+F22CF1−F2DF1+F2
A2(F1+F2)BF1+F22CF1−F2DF1+F2 - Question 3 - Select One
In a triangle ABC three forces of magnitudes 3−−→AB,2−−→AC and 6−−→CB are acting along the sides AB, AC and CB respectively . If the resultant meets AC at D, then the ratio DC: AD will be equal to
A1:1B1:2C1:3D1:4
ABC is an equilateral triangle with O as its centre −→F1,−→F2 and −→F3 represent three forces acting along the sides AB, BC and AC respectively. If the torque about O is zero then the magnitude of −→F3 is
 View Solution
View SolutionIf f is the centre of a circle inscribed in a triangle ABC, then ∣∣∣−−→BC∣∣∣−→IA+∣∣∣−−→CA∣∣∣−→IB+∣∣∣−−→AB∣∣∣−→IC is
View SolutionOrthocenter of an equilateral triangle ABC is the origin O. If −−→OA=→a,−−→OB=→b,−−→OC=→c, then −−→AB+2−−→BC+3−−→CA=
View SolutionTwo forces →F1=3ˆi+4ˆj and →F2=3ˆj+4ˆk are acting simultaneously at a point. What is the magnitude of the resultant force ?
View SolutionOrthocenter of an equilateral triangle ABC is the origin O. If −−→OA=→a,−−→OB=→b,−−→OC=→c, then −−→AB+2−−→BC+3−−→CA=
View Solution

