On a piece of paper certain odd number of horizontal lines at equal distances are drawn. An equal number of vertical lines at equal distances are also drawn, forming rectangles. The rectangles are coloured black or white, set alternately. Three coins are put at random in these rectangles. Let p be the probability of having two coins in rectangles of the same colour and the third in a rectangle of the other colour, and p' be the probability of having all the coins in the rectangles of the same colour. If p:p'=16:5 then find the number of horizontal lines drawn on the paper.
Video Solution
Text Solution
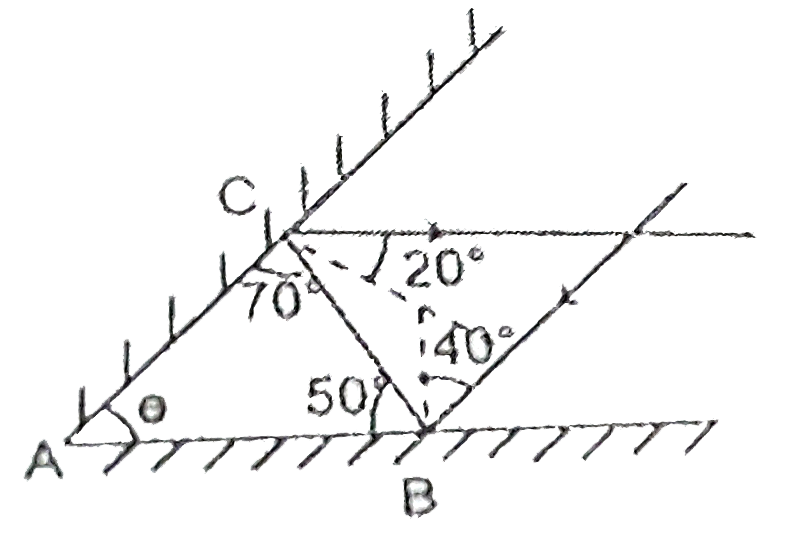
In ΔABC
∠ABC=50∘
∠ACB=70∘
But ∠ACB+∠ABC+∠CAB=180∘
70+50+∠CAB=180∘
∠CAB=180−120=60∘
n=360∘θ−1=360∘60∘−1=6−1=5
|
Topper's Solved these Questions
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - Level 3
5 Videos
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - TEST 1
15 Videos
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - Level 1
44 Videos
- KINEMATICSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - KINEMATICSEXERCISE - ASSESSMENT TEST (TEST 2 (SELECT THE CORRECT ALTERNATIVE)
15 Videos
- MACHINES AND TOOLSBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MACHINES AND TOOLSEXERCISE - CONCEPT APPLICATION (LEVEL 2)
12 Videos
Similar Questions
Knowledge Check
The perimeter of a rectangle and an equilateral triangle are same. Also, one of the sides of the rectangle is equal to the side of the triangle. The ratio of the areas of the rectangle and the triangle is
A√3:1B1:√3C2:√3D4:√3The perimeter of a rectangle and an equilateral triangle are same. Also, one of the sides of the rectangle is equal to the side of the triangle. The ratio of the areas of the rectangle and the triangle is
A√3:1B1:√3C2:√3D4:√3The perimeter of a rectangle and an equilateral triangle are same. Also , one of the sides of the rectangle is equal to the side of the triangle. The ratio of the areas of the rectangle and the triangle is :
A√3:1B1:√3C2:√3D4:√3
PQRS is a rectangle. State the lines of symmetry of the rectangle.
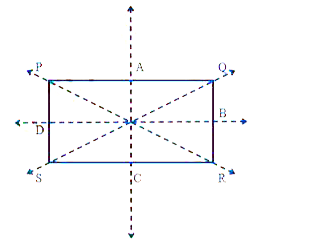
View SolutionLines of symmetry of a rectangle
View SolutionLines of symmetry of a rectangle
View SolutionProve that the diagonals of a rectangle bisect each other and are equal.
View SolutionIf the perimeters of a rectangle and a square are equal and the ratio of two adjacent sides of the rectangle is 1:2 then the ratio of area of the rectangle and that of the square is
View Solution
