On the opposite sides of a wide vertical vessel filled with water, two identical holes are opened, each having cross sectiona area a. The height dference between them is equal to . Find the resultant force of reaction of water flowing out of vessel.
To find the resultant force of reaction of water flowing out of a vertical vessel through two identical holes at different heights, we can follow these steps:
Step 1: Understand the Setup
We have a vertical vessel filled with water. There are two holes (A and B) on opposite sides of the vessel, with a height difference h between them. Each hole has a cross-sectional area a.
Step 2: Apply Bernoulli's Equation
Using Bernoulli's theorem, we can relate the velocities of the water flowing out of the holes to the height difference. The equation states that:
Pa+ρghA+12ρV2A=Pb+ρghB+12ρV2B
Where:
- Pa and Pb are the pressures at points A and B (both atmospheric pressure, hence they cancel out).
- hA and hB are the heights of points A and B respectively.
- VA and VB are the velocities of water at points A and B.
Step 3: Establish the Heights
Assuming hA=0 (the reference point) and hB=h, we can simplify the equation to:
ρgh+12ρV2B=12ρV2A
Step 4: Solve for Velocity Difference
Rearranging gives us:
V2B−V2A=2gh
Step 5: Calculate the Forces
The force exerted by the water flowing out of each hole can be calculated using the formula:
F=ρAV2
For hole A, the force FA is:
FA=ρaV2A
For hole B, the force FB is:
FB=ρaV2B
Step 6: Find the Resultant Force
The net force Fnet acting on the vessel due to the water flowing out of both holes is:
Fnet=FB−FA=ρa(V2B−V2A)
Substituting V2B−V2A=2gh:
Fnet=ρa(2gh)
Step 7: Final Result
Thus, the resultant force of reaction of water flowing out of the vessel is:
Fnet=2ρgah
We have a vertical vessel filled with water. There are two holes (A and B) on opposite sides of the vessel, with a height difference h between them. Each hole has a cross-sectional area a.
Using Bernoulli's theorem, we can relate the velocities of the water flowing out of the holes to the height difference. The equation states that:
- Pa and Pb are the pressures at points A and B (both atmospheric pressure, hence they cancel out).
- hA and hB are the heights of points A and B respectively.
- VA and VB are the velocities of water at points A and B.
Assuming hA=0 (the reference point) and hB=h, we can simplify the equation to:
Rearranging gives us:
The force exerted by the water flowing out of each hole can be calculated using the formula:
The net force Fnet acting on the vessel due to the water flowing out of both holes is:
Thus, the resultant force of reaction of water flowing out of the vessel is:
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
On the opposite sides of vertical vessel filled with water, two identical holes are opened. If area of cross-section for each is a and difference of height of these two is h and p is density of water, then force on the vessel is
View SolutionThere are two holes one each along the opposite sides of a wide rectangular tank. The cross section of each hole is 0.01m2 and the vertical distance between the holes is one meter. The tank is filled with water. The net force on the tank in newton when water flows out of the holes is (density of water 1000kg/m3)
View SolutionA fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
View SolutionA vessel having perfectly reflecting plane botton is filled with water (μ=4/3) to depth d. A point source of light is placed at a height h above the surface of water. Find the distance of final image from water surface.
View SolutionA cylindrical container of radius 'R' and height 'h' is completely filled with a liquid. Two horizontal L-shaped pipes of small cross-sectional area 'a' are connected to the cylinder as shown in the figure. Now the two pipes are opened and fluid starts coming out of the pipes horizontally in opposite directions. Then the torque due to ejected liquid on the system is

View SolutionThe side wall of a wide vertical vessel of height h=75cm a narrow slit (vertical) running all the way down to the bottom of the vessel.
The length of the slit is l=50cm and the width is b=1mm. With the slit closed, water is filled to the top. Find the resultant reaction force of water coming out as the slit is opened. brgt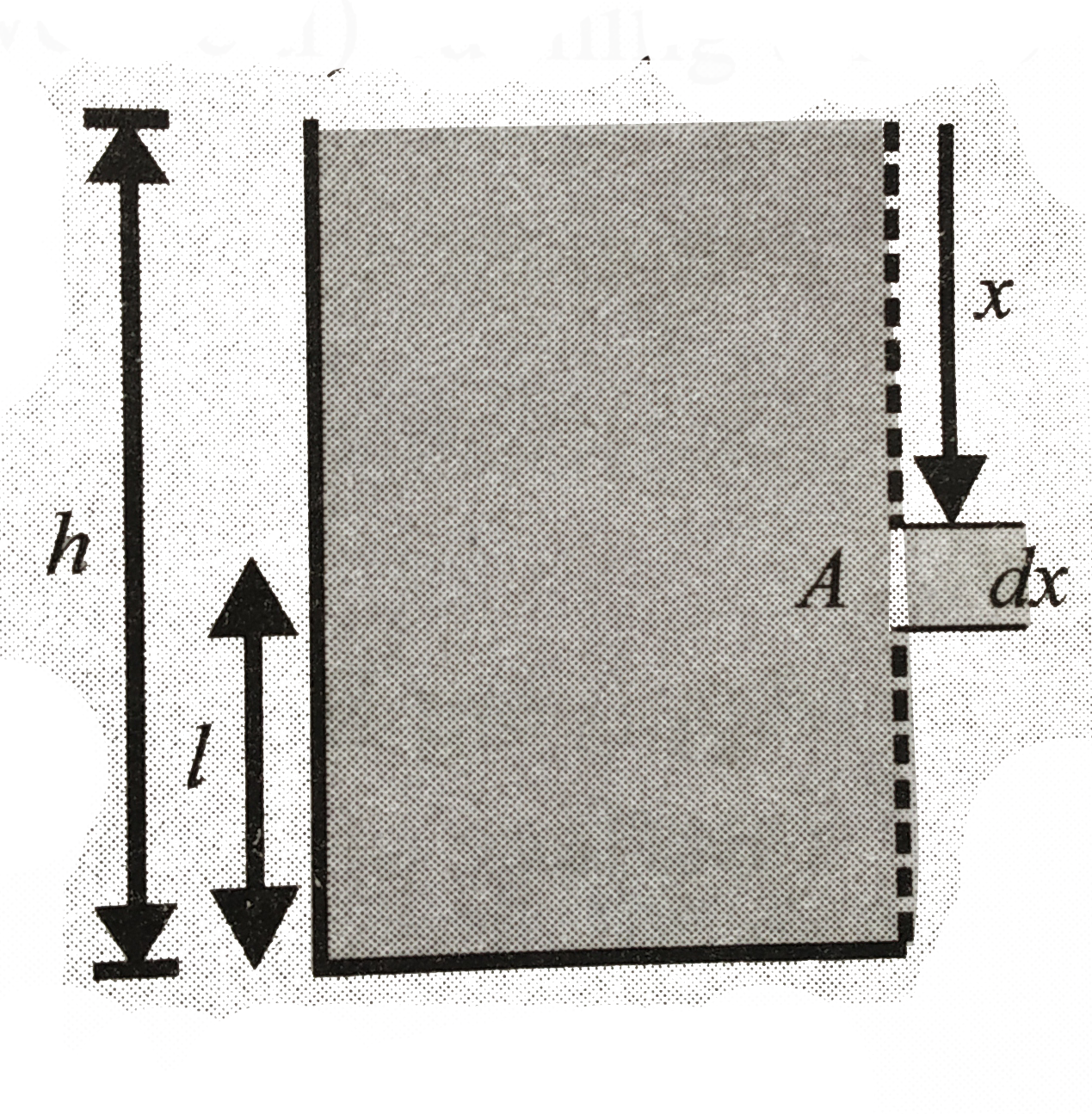
View SolutionWater drains out of a vessel filled with water upto height h through a hole of area A in t seconds.If the height of the water is 4 h then how much time will be required for the water to drain out ?[Assume A<<A0 (area of tank ) ]
View SolutionA tank of height H and base area A is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area A3 and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
After long time, when the height of water inside the tank again becomes equal to H2, the solid cylinder is taken out. then the velocity of liquid flowing out of the orifice (just after removing the cylinder) will be
View SolutionA vessel in the form of inverted cone. Its height is 8 cm and radius of its top, which is open, is 5 cm. It is filled with water upto the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped in the vessel, one fourth of the water flows out. Find the number of lead shots dropped in the vessel.
View SolutionA vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
View Solution
