One end of a long string of linear mass dnesity 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256 Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0 the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describest the wave on the string.
The equation of a travelling wave propagating along the positive y-direction is given by the displacement equation:
y(x,t)=asin(wt−kx)...(i)
Linear mass density, μ=8.0×10−3kgm−1
Frequency of the tuning fork, v=256 HZ
Amplitude of the wave, a = 5.0 cm = 0.05 m … (ii)
Mass of the pan, m = 90 kg
Tension in the string, T=mg=90×9.8=882N
The velocity of the transverse wave v, is given by the relation:
v=√Tμ
=√8828.0×10−3=332m/s
Angular frequency ω=2πv
=2×3.14×256
=1608.5=1.6×103rad/s.....(iii)
Wavelength λ=vv=332256m
∴ Propagation constant , k=2πλ
=2×3.14332256=4.84m−1.....(iv)
Substituting the values from equations (ii), (iii), and (iv) in equation (i), we get the displacement equation:
y(x,t)=0.05sin(1.6×103t−4.84×)m
Topper's Solved these Questions
Similar Questions
One end of a long string of linear mass density 10−2kgm−1 is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
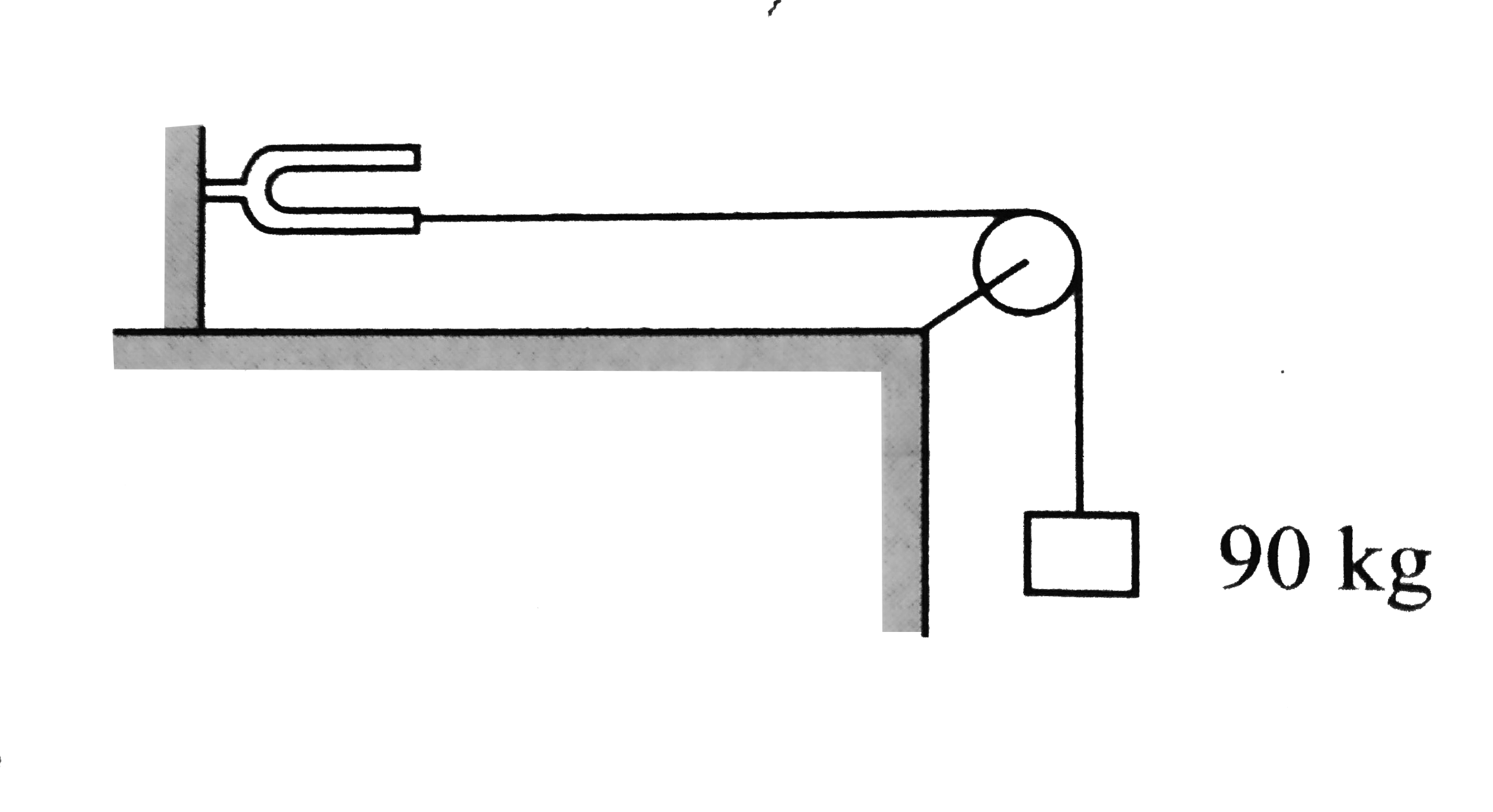
View SolutionOne end of a long string of linear mass density 10−2kgm−1 is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.

View Solution
Knowledge Check
If a string fixed at both ends having fundamental frequency of 240Hz is vibrated with the help of a tuning fork having frequency 280Hz, then the
Astring will vibrate with a frequency of 240HzBstring will be in resonance with the tuning forkCstring will vibrate with the frequency of tuning fork , but resonance condition will not be achievedDstring will vibrate with a frequency of 260Hz.A string fixed at both ends whose fundamental frequency is 240Hz is vibrated with the help of a tuning fork having frequency 480Hz, then
AThe string will vibrate with a frequency of 240HzBThe string will vibrate in resonance with the tuning forkCThe string will vibrate in resonance with a frequency of 480Hz, but is not a resonance with the tuning forkDThe string is in resonance with the tuning fork and hence vibrate with a frequency of 240HzA light string passes over a frictionless pulley. To one of its ends a mass of 6 kg is attached. To its other end a mass of 10 kg is attached. The tension in the thread will be
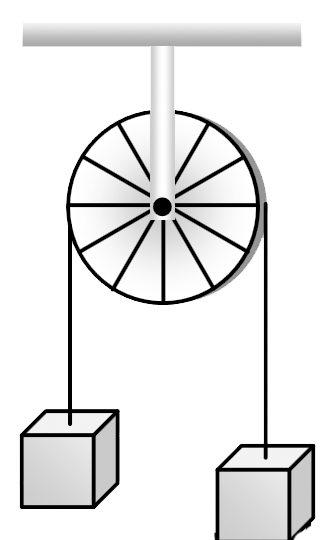 A24.5 NB2.45 NC79 ND73.5 N
A24.5 NB2.45 NC79 ND73.5 N
A tuning fork of frequency 250 Hz is vibrating at one end of a tube as shown in the figure. If maximum sound is heard at the other end, then the velocity of the waves will be

View SolutionOne end of a horizontal rope is attached to a prong of an electrically driven fork that vibrates at 120Hz. The other end passes over a pulley and supports a 1.50kg mass. The linear mass density of the rope is 0.0550kg/m.
(a) What is the speed of a transverse wave on the rope?
(b) Whatis the wavelength?
How would your answer to parts (a) and (b) change if the mass were increased to 3.00kg?
View SolutionOne end of a horizontal rope is attached to a prong of an electrically driven fork that vibrates at 120Hz. The other end passes over a pulley and supports a 1.50kg mass. The linear mass density of the rope is 0.0550kg/m.
(a) What is the speed of a transverse wave on the rope?
(b) Whatis the wavelength?
How would your answer to parts (a) and (b) change if the mass were increased to 3.00kg?
View SolutionIf a string fixed at both ends having fundamental frequency of 240Hz is vibrated with the help of a tuning fork having frequency 280Hz, then the
View SolutionA string fixed at both ends whose fundamental frequency is 240Hz is vibrated with the help of a tuning fork having frequency 480Hz, then
View Solution
