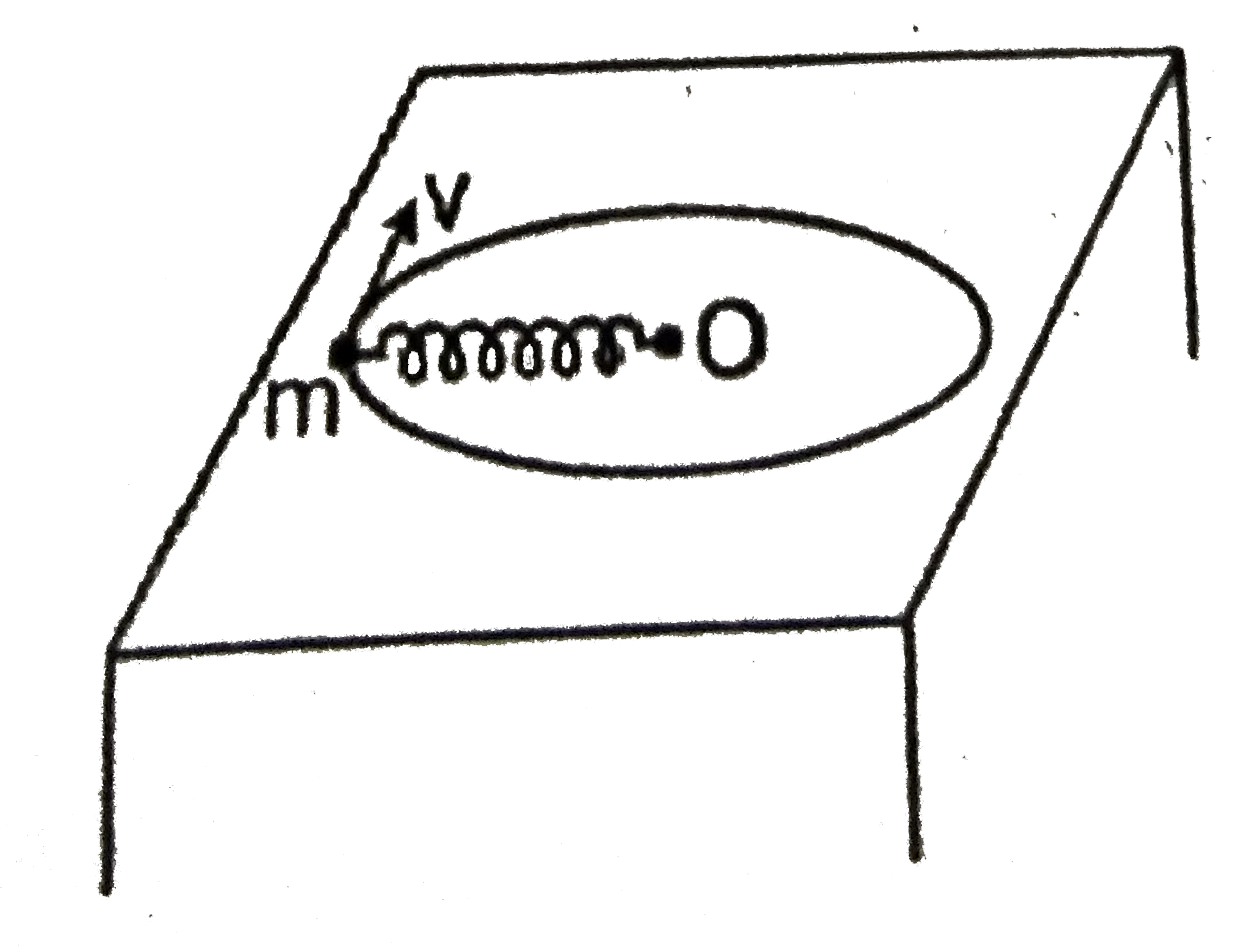
One end of a massless spring of spring constant 100 N/m and natural length 0.5 m is fixed and the other end is connected to a particle of mass 0.5 kg lying on as frictionless horizontal table. The spring remains horizontal. If the mass is made to rotate at an angular velocity of 2 rad/s, find the elongation of the spring.Solution in Tamil
The particle is moving in a horizontal circle so it si accelerated towards the centre with magnitude v2r. The horizontal foce on the particle is due toteh spring and equals kl, where l is the elongation and k is the spring constant. Thus
kl=mv2r=mω2=mω2(l0+l).
Here omega is the angular velocity l0 is theN/Atural length (0.5m) and l0+l is the total length of the spring which is also the radius of the circle along which the particle moves.
Thus,(k−mω2)=mω2l0
orl=mω2l0k−mω2
Putting the values
l=0.5×4×0.5100−0.5×4m≈1100m=1cm.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer10videos
CIRCULAR MOTION
- BOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective -116videos
CIRCULAR MOTION
- BOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises30videos
CIRCULAR MOTION
- BOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises64videos
CENTRE OF MASS, LINEAR MOMENTUM, COLLISION
- BOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - All Questions96videos
FLUID MECHANICS
Similar Questions
You are driving a motorcycle ona horizontal raod. It is moving with a uniform velocity. Is it possibel to accelerate the motorcycle wilthout putting higher petrol input rate into the engine?
04:45View SolutionWhen a particle moves in a circle with a uniform speed
03:46View SolutionFind the accelerationof the moon with respect to the eath from the following data, Distance between the earth and the moon =3.85×105 km and the time taken by the moon to complete one revolution around the earth =27.3days
03:28View SolutionThree particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
02:02View SolutionWater is filled in a flask up to a height of 20 cm. The bottom of the flask is circular with radius 10 cm. If the atmospheric pressure is 1.01×105 Pa, find the force exerted by the water on the bottom. Take g=10ms−2 and density of water =1000 kgm^-3.
03:21View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards abnother block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 The spring constant of the spring fixed at one end is 10 N/m. Find the maximum compression of the spring.
04:02View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
04:14View SolutionOne end of an ideal spring of unstreched length l_(O)=1m , is fixed on a frictionless horizontal table. The other end has a small disc of mass 0.1 kg attached to it. The disc is projected with a velocity upsilon_(0)=11 m//s perpendicular to the spring. What is the force constant of spring?
View SolutionMass m is connected with an ideal spring of natural length l whose other end is fixed on a smooth horizontal table. Initially spring is in its natural length l. Mass m is given a velocity 'v' perpendicular to the spring and released . The velocity perpendicular to the spring when its length l+x , will be
 04:24View Solution
04:24View Solutionकिसी घर्षण रहित क्षैतिज मेज पर 1 मीटर लम्बाई की स्प्रिंग (k = 100 न्यूटन/मीटर) का एक सिरा स्थिर हैं तथा दूसरा सिरा 1 किग्रा द्रव्यमान से जुड़ा हैं । यदि द्रव्यमान को 2 रेडियन / सेकण्ड के कोणीय वेग से क्षैतिज तल में घुमाया जाये तो स्प्रिंग की लम्बाई में वृध्दि ज्ञात कीजियें ।
02:57View Solutionएक द्रव्यमानरहित स्प्रिंग नियतांक 100 N/m है और स्वाभाविक लंबाई 0.5 m है। इसका एक सिरा एक घर्षणरहित क्षैतिज मेज के एक बिंदु पर स्थिर है और दूसरा सिरा 0.5 kg द्रव्यमान का कण से जुड़ा है। यह कण मेज पर 2 rad/s के कोणीय वेग से वृत्ताकार पथ पर है। लंबाई में वृद्धि ज्ञात करे।
07:02View SolutionA body of mass m is tied to one end of a spring and whirled round in a horizontal circle with a constant angular velocity .The elongation is 1 cm . If the angular velocity is doubled , the elongation in the spring is 5 cm. what is the original length of the spring ?
View SolutionOne end of a massless spring of spring constant 100 Nm^(-1) and natural length 0.5 m is fixed and the other end is connected to a particle of mass 0.5 kg lying on a frictionless horizontal table. If the mass rotates at an angular velocity of 2 rad s^(-1) , the elongation of the spring is approximately.
04:14View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.
 View Solution
View SolutionA block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
03:34View SolutionA massless spring of natural length of 0.5 m and spring constant 50 N/m has one end fixed and the other end attached to a mass of 250 g. The spring mass system is on a smooth floor. The mass is pulled until the length of the spring is 0.6 m and then released from rest. The kinetic energy of the mass when the length of the spring is 0.5 m is
03:08View Solution

