One mole of an ideal monatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate
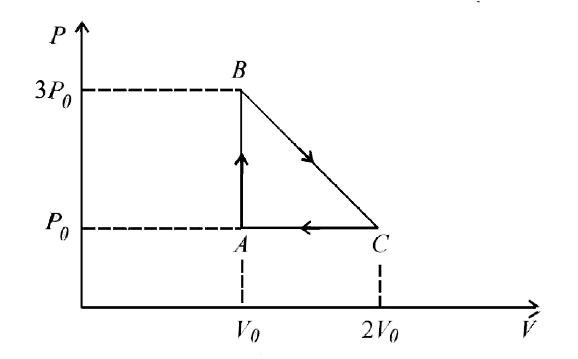
(a) the work done by the gas.
(b) the heat rejected by the gas in the path CA and the heat absorbed by the gas in the path AB,
(c) the net heat absorbed by the gas in the path BC,
(d) the maximum temperature attained by the gas during the cycle.
a. The work done by the gas is equal to the area under the closed curve. Thus, work done in cycle is
W=12(2V0−V0)(3P0−P0)
=12V0×2P0=P0V0
b. Heat rejected in path CA is given as
QCA=nCPΔT=nCP(TC−TA)
=1×(5/2)R[P02V0R−P0V0R]=52P0V0
(as n = 1 mole)
Heat absorbed in path AC is
QAC=nCP(TB−TA)
=1×32R×[3P0V0R−P0V0R]=3P0V0
For cycle ABC, we have
heat supplied = work done by the gas
or −(52)P0V0+3P0V0+QBC=P0V0
Heat supplied to path BC is given by
QBC=P0V0+(52)P0V0−3P0V0=P0V0/2
d. We know that PV/T = constant. So, when PV is maximum, T is also maximum. PV is maximum for part BC. Hence, temperature will be maximum between B and C.
Let equation of BC be
P=kV+k'
satisfying both the point B and C
Fro point C,
3P0=V0+k'
For point C,
P0=k(2V0)+k'
Solving these equations, we get
k=−2(P0/V0) and k'=5P0
So the equation for time BC is
P=−2(P0V0)×V+5P0
or (RTV)=−(2P0VV0)+5P0
or T=P0R[5V−2(v2V0)]=0
For maximum, dT/dV=0
So (dTdV)=(P0R)[5−(4VV0)]=0
Hence, 5−(4VV0)=0 or 5V0−4V=0
or V=(54)V0
Substituting the value fo V from Eq. (ii) in Eq. (i) we get
Tanmax=P0R[5×(54V0)−2(5V04)21V0]=P0R[25V04−25V08]
=P0R×25V08=25P0V08R
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.120videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.228videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger11videos
KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICS
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
- BOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type9videos
LINEAR AND ANGULAR SIMPLE HARMONIC MOTION
Similar Questions
One mole of ideal monatomic gas in taken in cyclice process ABCA as shown in the figure

Calculate :
(a) The work done by the gas
(b) The heat rejected by the gas in the path CA
(c) The net heat absorbed be the by gas in the path BC
(d) Maximum temperature obtained by the gas during the cycle.View SolutionOne mole of monoatomic gas taken through a cyclic process as shown in figure.
Calculate ∑ABCA=dqrevT.View Solution
Knowledge Check
- Question 1 - Select One
One mole of an ideal mono-atomic gas is taken round cyclic process ABCD as shown in figure below. Calculate
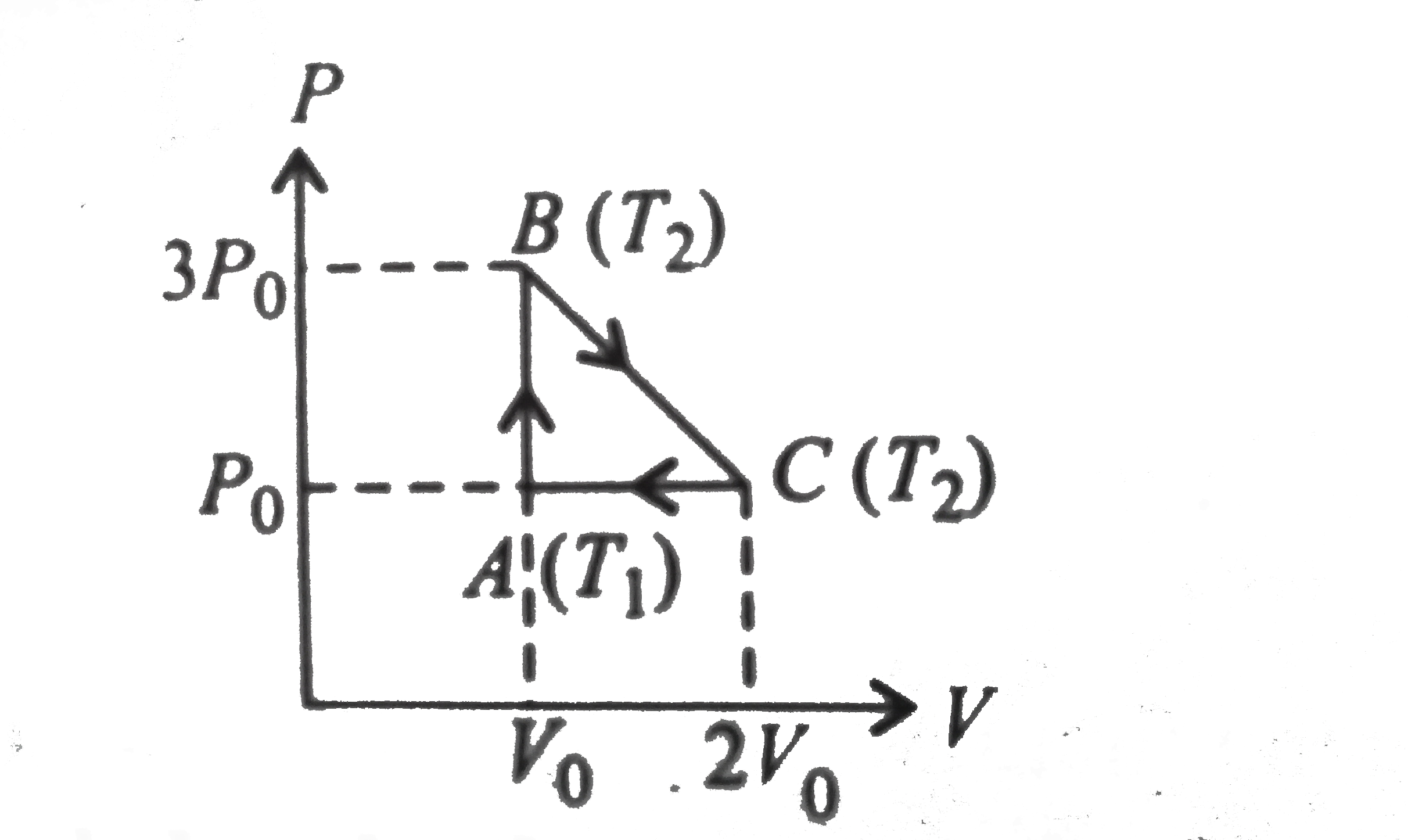 AThe work done by the gas.BThe heat rejected by the gas in the path CAand the heat absorbed by the gas in the path AB.CThe net heat absorbed by the gas in the path BC.DThe maixmum temperature attained by the gas during the cycle.
AThe work done by the gas.BThe heat rejected by the gas in the path CAand the heat absorbed by the gas in the path AB.CThe net heat absorbed by the gas in the path BC.DThe maixmum temperature attained by the gas during the cycle. - Question 2 - Select One
One mole of ideal monoatmic gas is carried throught the reversible cyclic process as shown in figure. Calculate net heat absorbed by the gas in the path BC
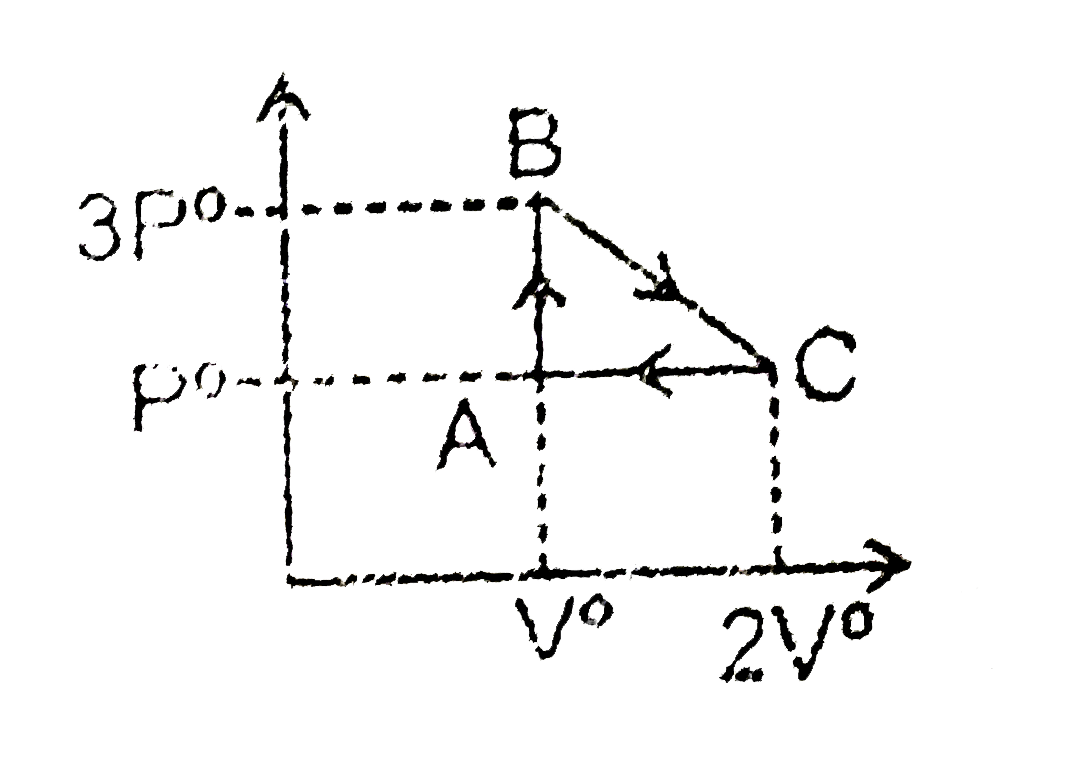 A12P∘V∘B72P∘V∘C2P∘V∘D52P∘V∘
A12P∘V∘B72P∘V∘C2P∘V∘D52P∘V∘ - Question 3 - Select One
One mole of ideal monatomic gas is carried through the reversible cyclic process as shown in figure. Calculate the max temperature attained by the gas during the cycle.
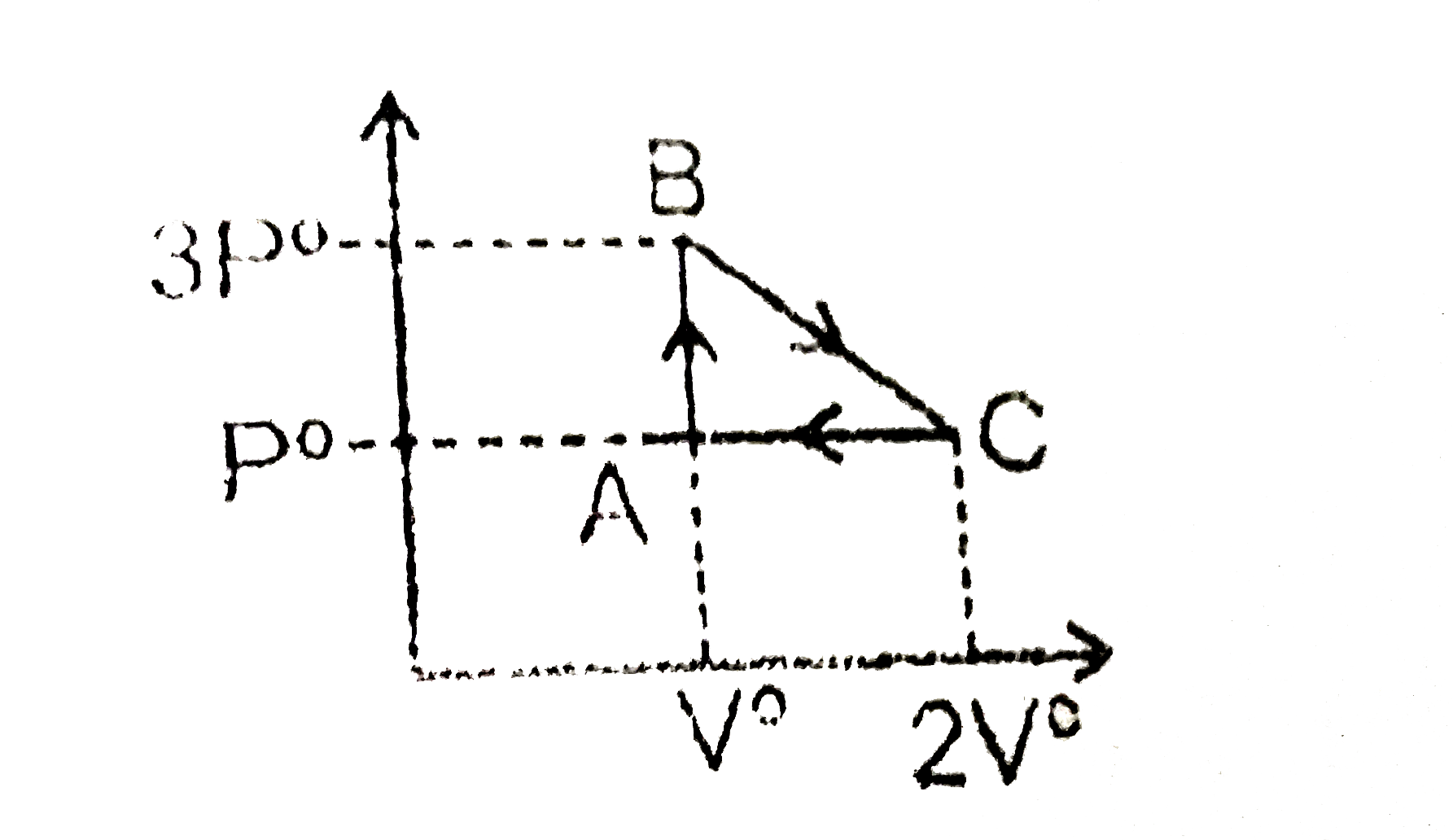 A258(P∘V∘R)B−258(P∘V∘R)C358(P∘V∘R)D−358(P∘V∘R)
A258(P∘V∘R)B−258(P∘V∘R)C358(P∘V∘R)D−358(P∘V∘R)
One mole of monoatomic gas is taken round the cyclic process. Heat absorbed by gas in process AB is
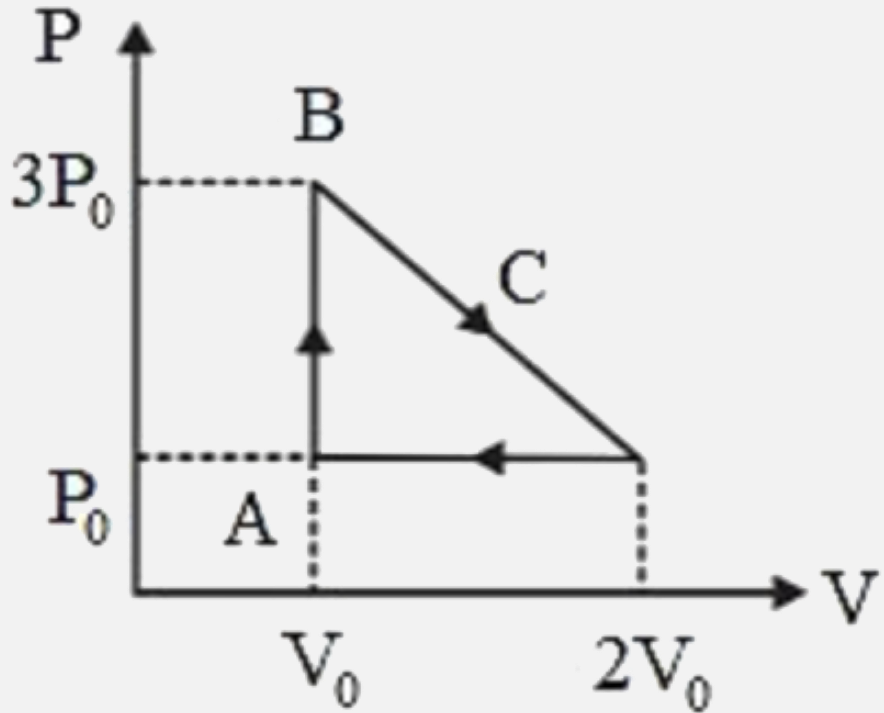 View Solution
View SolutionOne mole of ideal monoatomic gas is taken round the cyclic process as shown in figure.
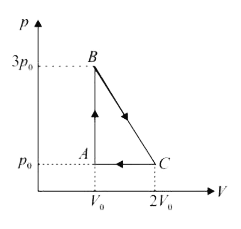
The heat rejected by the gas in the path is ………...and the heat absorbed by the gas in the path AB is ………...........View SolutionTwo moles of an ideal monoatomic gas undergoes a cyclic process ABCA as shown in V-T diagram below:

Work done by the gas during the entire cycle is :View SolutionOne mole of a monatomic ideal gas is taken along the cycle ABCA as shown in the diagram.
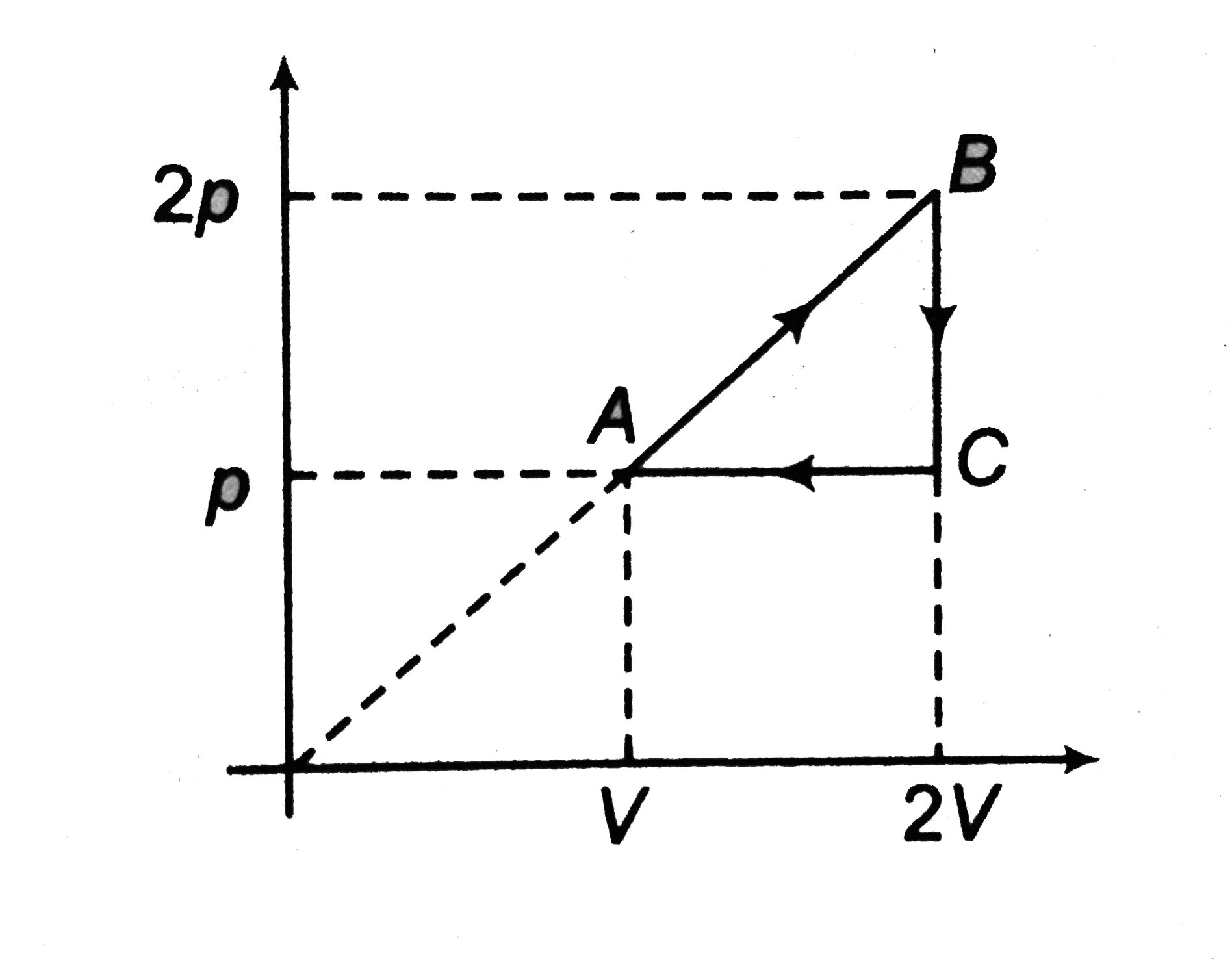
The net heat absorbed by the gas in the given cycle isView SolutionTwo moles of helium gas undergo a cyclic process as shown in figure. Assuming the gas to be ideal. The net work done by the gas is
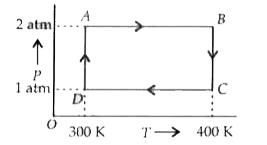 View Solution
View Solution

