One side of radius of curvature R2=120cm of a convexo-convex lens of material of refractive index μ=1.5 and focal length f1=40cm is slivered. It is placed on a horizontal surface with silvered surface in contact with it. Another convex lens of focal length f2=20cm is fixed coaxially d=10cm above the first lens. A luminous point object O on the axis gives rise to an image coincide with it. Find its height above the upper lens.
The correct Answer is:A, C
To solve the problem step by step, we will follow the given information and apply the lens maker's formula and the lens formula.
Step 1: Understand the Configuration
We have two convex lenses:
- Lens L1 (the lower lens) has a focal length f1=40cm and a radius of curvature R1=120cm (the silvered side is the second surface).
- Lens L2 (the upper lens) has a focal length f2=20cm.
- The distance between the two lenses is d=10cm.
Step 2: Calculate the Radius of Curvature for L1
Using the lens maker's formula:
1f=μ−1(1R1−1R2)
For lens L1:
- f1=40cm
- μ=1.5
- R1=120cm (convex, hence positive)
We need to find R2:
140=1.5−1(1120−1R2)
140=0.5(1120−1R2)
Multiplying both sides by 2:
120=1120−1R2
Rearranging gives:
1R2=1120−120
Finding a common denominator (120):
1R2=1120−6120=−5120
Thus,
R2=−24cm
Step 3: Calculate the Image Distance for L1
Using the lens formula for L1:
1f1=1v1−1u1
Where u1 is the object distance from L1. Since the object is a luminous point, we can assume u1 is negative (real object):
140=1v1−1u1
Assuming u1=−x (where x is the distance from the object to L1):
140=1v1+1x
Step 4: Calculate the Image Distance for L2
For lens L2, the image formed by L1 acts as the object for L2. The distance of the image from L1 to L2 is d=10cm, thus:
u2=v1−10
Using the lens formula for L2:
1f2=1v2−1u2
Substituting f2=20:
120=1v2−1(v1−10)
Step 5: Solve for Object and Image Distances
Since the image coincides with the object, we have v2=−x. Therefore, substituting v2 into the equation gives:
120=−1x−1(v1−10)
Now we solve for x.
Step 6: Calculate Height Above the Upper Lens
The height of the image above the upper lens can be calculated using the magnification formula:
h=ho⋅v2u2
Where ho is the height of the object.
Final Calculation
After calculating the distances and substituting back, we find the height above the upper lens.
We have two convex lenses:
- Lens L1 (the lower lens) has a focal length f1=40cm and a radius of curvature R1=120cm (the silvered side is the second surface).
- Lens L2 (the upper lens) has a focal length f2=20cm.
- The distance between the two lenses is d=10cm.
Using the lens maker's formula:
1f=μ−1(1R1−1R2)
For lens L1:
- f1=40cm
- μ=1.5
- R1=120cm (convex, hence positive)
140=1.5−1(1120−1R2)
140=0.5(1120−1R2)
Multiplying both sides by 2:
120=1120−1R2
Rearranging gives:
1R2=1120−120
Finding a common denominator (120):
1R2=1120−6120=−5120
Thus,
R2=−24cm
Using the lens formula for L1:
1f1=1v1−1u1
Where u1 is the object distance from L1. Since the object is a luminous point, we can assume u1 is negative (real object):
140=1v1−1u1
Assuming u1=−x (where x is the distance from the object to L1):
140=1v1+1x
For lens L2, the image formed by L1 acts as the object for L2. The distance of the image from L1 to L2 is d=10cm, thus:
u2=v1−10
Using the lens formula for L2:
1f2=1v2−1u2
Substituting f2=20:
120=1v2−1(v1−10)
Since the image coincides with the object, we have v2=−x. Therefore, substituting v2 into the equation gives:
120=−1x−1(v1−10)
Now we solve for x.
The height of the image above the upper lens can be calculated using the magnification formula:
h=ho⋅v2u2
Where ho is the height of the object.
After calculating the distances and substituting back, we find the height above the upper lens.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Comprehension Based
3 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
A convex lens of focal length 40cm is held at a distance 12cm coaxially above a concave mirror of focale length 18cm.
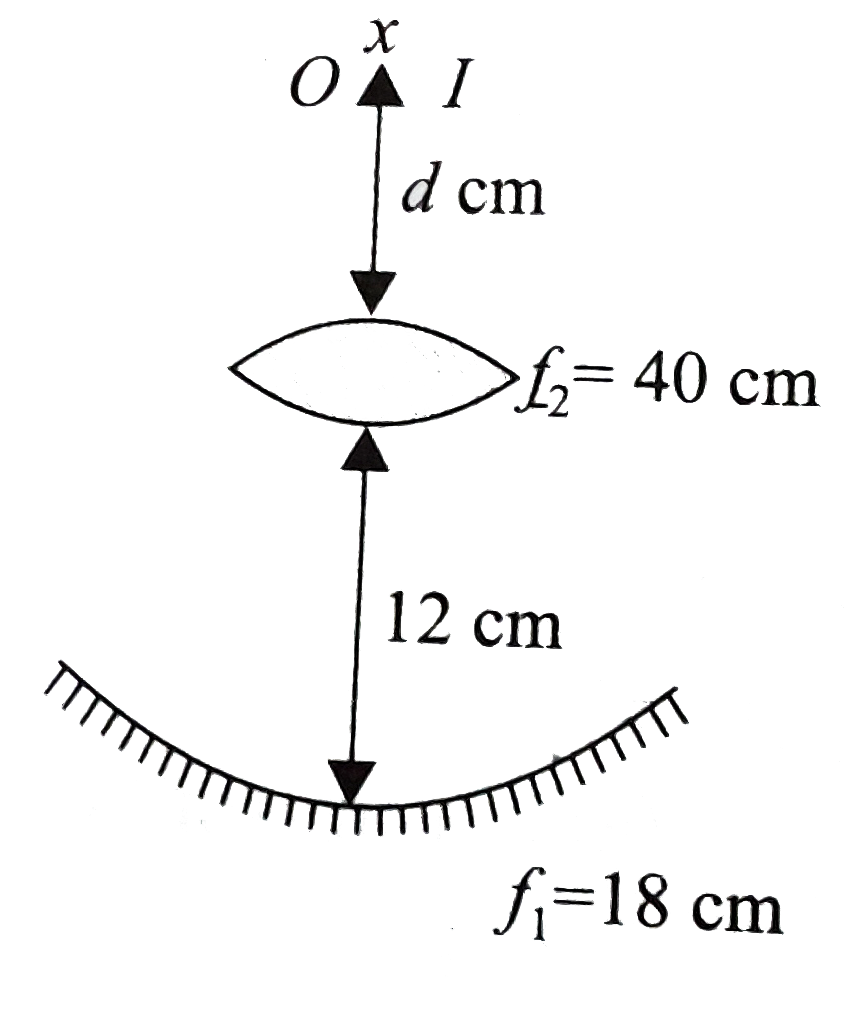
Q. A luminous point object placed d cm above the lens on its axis gives rise to an imag coincident iwth itself, then the value of d is equal to
View SolutionThe radius of curvature of curved surface of a thin plano-convex lens is 10cm and the refractive index is 1.5. If the plano surface is silvered, then the focal length will be.
View Solution
Knowledge Check
The radius curvature of each surface of a convex lens of refractive index 1.5 is 40 cm. Calculate its power.
A2.5DB2DC1.5DD1D
A planocovex lens is made of a material of refractive in μ=1.5 The radius of curvature of curved surface of the lens is 20.cm. If its plane surface3 is silvered, the focal length of the silvered lens will be
View SolutionA convexo-concave convergent lens is made of glass of refractive index 1.5 and focal length 24cm. Radius of curvature for one surface is double than that of the other. Then,radii of curvature for the two surfaces are (in cm)
View SolutionA convex-concave diverging lens is made of glass of refractive index 1.5 and focal length 24 cm. radius of curvature for one surface is double that of the other. Then radii of curvature for the two surfaces are (in cm )
View SolutionThe radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
View SolutionFocal length of a convex lens of refractive index 1.5 is 2 cm. Focal length of lens when immersed in a liquid of refractive index 1.25 will be
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View SolutionA plano convex lens of radius of curvature 30 cm and refractive index 1.5 is kept in air. Find its focal length (in cm).
View Solution
