Optic axis of a thin equi-convex lens is the x-axis. The co-ordinates of a point object and its image are (−40cm,1cm)and(50cm,−2cm), respectively. Lens is located at
x=20cm
x=−30cm
x=−10cm
origin
The correct Answer is:C
To find the location of the lens based on the given coordinates of the object and its image, we can follow these steps:
Step 1: Identify the coordinates
The coordinates of the point object and its image are given as:
- Object (O): (-40 cm, 1 cm)
- Image (I): (50 cm, -2 cm)
Step 2: Determine the heights
From the coordinates, we can identify the heights:
- Height of the object (H_object) = 1 cm
- Height of the image (H_image) = -2 cm (the negative sign indicates that the image is inverted)
Step 3: Calculate the magnification (m)
Magnification (m) is given by the formula:
m=HimageHobject
Substituting the values:
m=−21=−2
Step 4: Relate object distance (u) and image distance (v)
The magnification can also be expressed in terms of object distance (u) and image distance (v):
m=−vu
From the magnification calculated:
−2=−vu
This leads to:
v=2u
Step 5: Determine the distances
Let the distance of the object from the lens be d1 and the distance of the image from the lens be d2. According to the problem:
d1+d2=90 cm
Since d1=−u and d2=v, we can substitute:
−u+2u=90
This simplifies to:
u=90 cm
Step 6: Calculate the image distance (v)
Now substituting u back into the equation for v:
v=2u=2×90=180 cm
Step 7: Determine the location of the lens
The object is located at −40 cm, and we have found u=30 cm (the distance from the lens to the object). Thus, the lens is located at:
Lens position=−40 cm+30 cm=−10 cm
Conclusion
Therefore, the lens is located at x=−10 cm.
---
The coordinates of the point object and its image are given as:
- Object (O): (-40 cm, 1 cm)
- Image (I): (50 cm, -2 cm)
From the coordinates, we can identify the heights:
- Height of the object (H_object) = 1 cm
- Height of the image (H_image) = -2 cm (the negative sign indicates that the image is inverted)
Magnification (m) is given by the formula:
m=HimageHobject
Substituting the values:
m=−21=−2
The magnification can also be expressed in terms of object distance (u) and image distance (v):
m=−vu
From the magnification calculated:
−2=−vu
This leads to:
v=2u
Let the distance of the object from the lens be d1 and the distance of the image from the lens be d2. According to the problem:
d1+d2=90 cm
Since d1=−u and d2=v, we can substitute:
−u+2u=90
This simplifies to:
u=90 cm
Now substituting u back into the equation for v:
v=2u=2×90=180 cm
The object is located at −40 cm, and we have found u=30 cm (the distance from the lens to the object). Thus, the lens is located at:
Lens position=−40 cm+30 cm=−10 cm
Therefore, the lens is located at x=−10 cm.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - more than one correct option
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions
8 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Optic axis of a thin equiconvex lens is the x-axis. The co-rodinates of a point object and its image axis (−40cm,1cm) and (50cm,−2cm) respectively. Lens is located at
View SolutionPlane surface of a thin plano-convex lens is silvered. If a point object is placed on principal axis at a distance 60cm from the lens and fial image is formed at a distance 30cm from the lens on same side. What will be the distance of final imagge from the lens if the plane surface is not silvered.
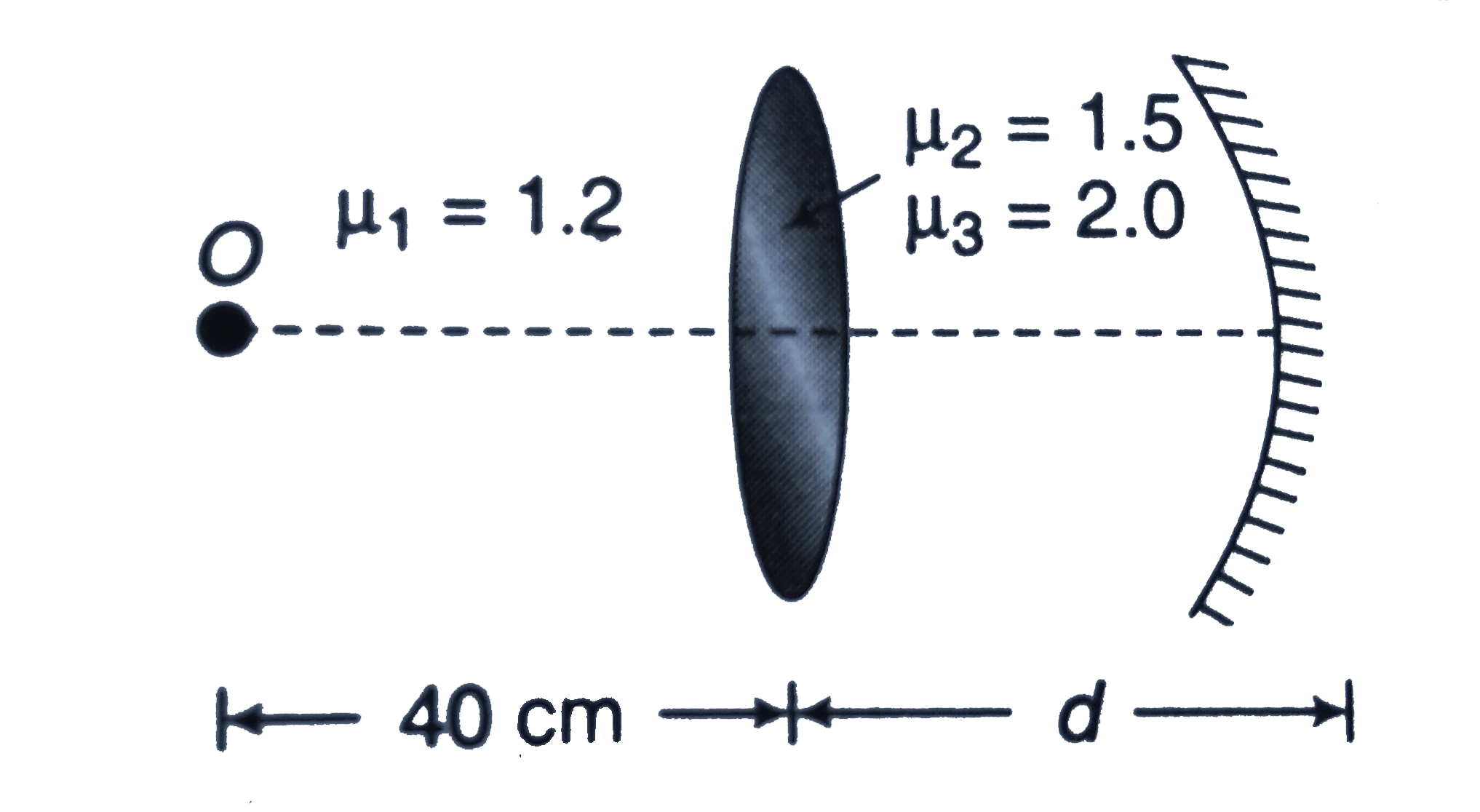
View SolutionThe figure shows an arrangement of an equi-convex lens and a concave mirror. A point object O is placed on the principal axis at a distance 40cm from the lens such that the final image is also formed at the position of the object. If the radius of curvature of the concave mirror is 80cm, find the distance d. Also draw the ray diagram. The focal length of the lens in air is 20cm.
View SolutionTwo point objects are placed on principal axis of a thin converging lens. One is 20cm from the lens and other is on the other side of lens at a distance of 40 cm from the lens. The images of both objects coincide. The magnitude of focal length of lens is :-
View SolutionA 4 cm tall object is placed on the principal axis of a convex lens. The distance of the
object from the optical centre of the lens 12 cm and its sharp image is formed at a
distance of 24 cm from it on a screen on the lens, in the which ways (towards the lens or away from the lens) will he have to move the screen to get a sharp image of the object on it again? How will the magnification of the image be affected ? .
View SolutionIf the distances of an object and its virtual image from the focus of a convex lens of focal length f are 1 cm each, then f is
View SolutionIf the distances of an object and its virtual image from the focus of a convex lens of focal length f are 1 cm each, then f is
View SolutionWhen an object is placed 40cm from a diverging lens, its virtual image is formed 20cm from the lens. The focal length and power of lens are
View SolutionAn unsymmeterical double convex thin lens forms the image of a point object on its axis. Will the position of the image change if the lens is reversed ?
View SolutionA point source of light is kept at a distance of 15cm from a converging lens,on its optical axis.The focal length of the lens is 10cm and its diameter is 3cm ,A screen is placed on the other side of the lens ,perpendicular to the axis of lens,at a distance 20cm from it.Then find the area of the illuminated part of the screen?
View Solution
