Rain is falling vertically. A man running on the road keeps his umbrella tilted but a man standing on the street keeps his umbrella vertical to protect himself from the rain. But both of them keep their umbrella vertical to avoid the vertical sun-rays. Explain.
To solve the problem, we need to analyze the situation of the two men with respect to the rain and sunlight.
1. Understanding the Rainfall:
- The rain is falling vertically downwards with a certain velocity, which we can denote as Vr.
2. Analyzing the Man Running:
- The man who is running has a horizontal velocity, which we can denote as Vm.
- Since he is moving, the effective velocity of the rain relative to him is not just vertical; it combines both the vertical velocity of the rain and the horizontal velocity of the man.
- This results in a resultant velocity of the rain that is at an angle to the vertical. Therefore, to effectively shield himself from the rain, he must tilt his umbrella at this angle.
3. Analyzing the Man Standing Still:
- The man who is standing still has a velocity of 0 (i.e., Vm=0).
- In this case, the only velocity acting is that of the rain, which is vertical. Thus, he can keep his umbrella vertical to protect himself from the rain.
4. Considering Sunlight:
- When it comes to sunlight, the speed of light is extremely high compared to any human movement.
- Therefore, regardless of whether a person is moving or standing still, the light rays from the sun can be considered to be coming vertically downwards.
- In both cases (running or standing), the umbrella should be kept vertical to block the sunlight effectively since there is no relative motion involved with light.
Conclusion:
- The man running tilts his umbrella to counteract the angle of the rain's resultant velocity, while the man standing still keeps his umbrella vertical because the rain is falling straight down. For sunlight, both men keep their umbrellas vertical since the speed of light makes relative motion negligible.
- The rain is falling vertically downwards with a certain velocity, which we can denote as Vr.
- The man who is running has a horizontal velocity, which we can denote as Vm.
- Since he is moving, the effective velocity of the rain relative to him is not just vertical; it combines both the vertical velocity of the rain and the horizontal velocity of the man.
- This results in a resultant velocity of the rain that is at an angle to the vertical. Therefore, to effectively shield himself from the rain, he must tilt his umbrella at this angle.
- The man who is standing still has a velocity of 0 (i.e., Vm=0).
- In this case, the only velocity acting is that of the rain, which is vertical. Thus, he can keep his umbrella vertical to protect himself from the rain.
- When it comes to sunlight, the speed of light is extremely high compared to any human movement.
- Therefore, regardless of whether a person is moving or standing still, the light rays from the sun can be considered to be coming vertically downwards.
- In both cases (running or standing), the umbrella should be kept vertical to block the sunlight effectively since there is no relative motion involved with light.
- The man running tilts his umbrella to counteract the angle of the rain's resultant velocity, while the man standing still keeps his umbrella vertical because the rain is falling straight down. For sunlight, both men keep their umbrellas vertical since the speed of light makes relative motion negligible.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises51videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer14videos
PHYSICS AND MATHEMATICS
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
Similar Questions
A man runs along a horizontal road on a rainy day. His umbrella vertical in order to protect himself from the rain then rain actually
View SolutionA boy is running on a horizontal road with a velocity of 5 m/s. At what angle should he hold his umbrella in order to protect him self from the rain if the rain is falling vertically with a velocity of 10 m/s?
View SolutionWhen it is raining vertically down, to a man walking on road the velocity of rain appears to be 1.5 times his velocity. To protect himself from rain he should hold the umbrella at an angle θ to vertical. Then tanθ=
View SolutionA man is travelling at 10.8 kmph in a topless car on a rainy day. He holds an umbrella at an angle of 37∘ with the vertical to protect himself from rain which is falling vertically downwards. What is the velocity of the rain drop ?
View SolutionA man is coming down an incline of angle 30∘. When he walks with speed 2(√3)ms−1 he has to keep his umbrella vertical to protect himself from rain. The actual speed of rain is 5ms−1. At angle with vertical should he keep his umbrella when he is at rest so that he does not getb drenched ?
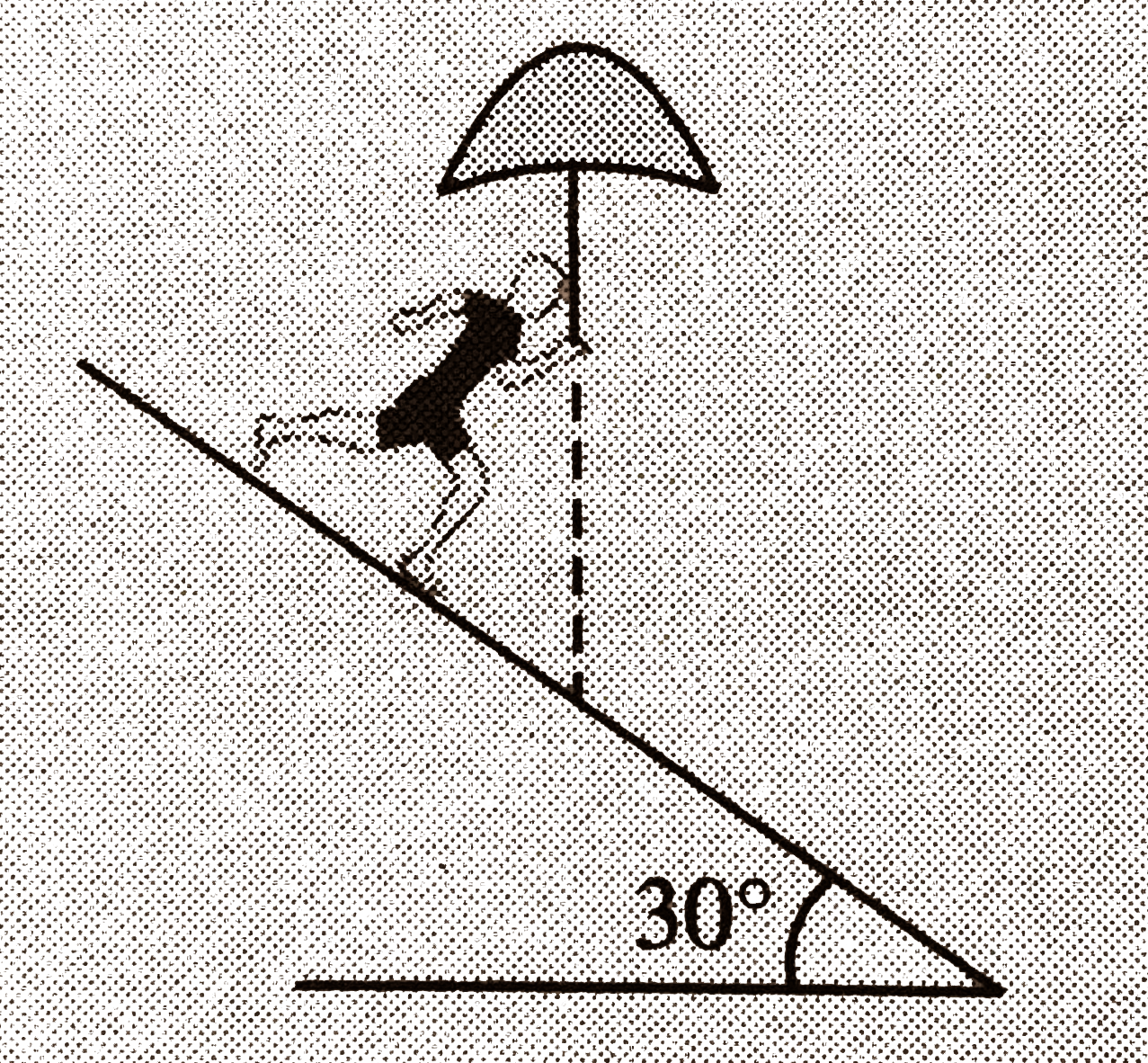 .View Solution
.View SolutionRain is falling vertically and a man is moving with velocity 6m/s find the angle with which umbrella should be held by man to avoid getting wet .
 View Solution
View SolutionStatement -1 : A man standing on the ground has to hold his umbrella at an angle θ with the vertical to protect himself from rain. It is possible that the man now starts running on the ground with certain speed, but he still has to hold his umbrella at angle θ with the vertical to protect himself from rain.
Statement -2 : Vertical component of velocity of rain w.r.t man does not change. if he starts running on a horizontal ground.View SolutionAssertion: Rain is falling vertically with a certain speed. A boy holding an umbrella rides a bicycle in east to west direction and does not get wet.
Reason: The boy is holding his umbrella (at some angles) with the vertical towards the west.View SolutionDuring a rainy day, rain is falling vertically with a velocity 2m/s A boy at rest starts his motion with a constant acceleration of 2m/s2 along a straight road . Find the rate at which the angle of the axis of umbrella with vertical should be changed so that the rain always falls parallel to the axis of the umbrella.
View SolutionRain is falling vertically with velocity 10m /s and a man is moving with velocity 6ms−1. Find the angle at which the man should hold his umbrella to above getting wet.
View Solution

