Read the following passage and then answer questions (a) to (e) on the basis of your under- standing of the passage and the related studied concepts.
In accordance with Faraday.s law of electromagnetic induction a magnetic field, changing with time, gives rise to an electric field. Again as per Ampere-Maxwell.s law an electric field, changing with time, gives rise to a magnetic field. It means that if we consider a charge oscillating with some frequency, it produces an oscillating electric field in space, which produces an oscillating mag- netic field, which in turn, is a source of oscillating electric field and so on. The oscillating electric and magnetic fields thus regenerate each other and an electromagnetic wave propagates through space. The energy associated with the propagating wave comes at the expense of the energy of the oscillating charge.
Electromagnetic wave propagates through free space as a transverse wave in which →Eand→B are perpendicular to each other as well as perpendicular to the direction of wave propagation. Like other waves electromagnetic waves carry energy and momentum. As electromagnetic waves contains both electric and magnetic fields, it has an electrical energy density μE=12∈0E2 as well as a magnetic energy density μB=B22μ0. Both of these vary with time.
Write an expression for the electric field.
(e ) The expression for the electric will be :
E2=60sin[1.5×1011t−0.5×103x]Vm−1
Topper's Solved these Questions
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - MULTIPLE CHOICE QUESTIONS25videos
ELECTROMAGNETIC WAVES
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - FILL IN THE BLANKS14videos
ELECTROMAGNETIC WAVES
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ADDITIONAL EXERCISES10videos
ELECTROMAGNETIC WAVES
- BOOK - U-LIKE SERIESCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - SELF ASSESSMENT TEST (SECTION-B) (VERY SHORT ANSWER QUESTIONS)4videos
ELECTRIC CHARGES AND FIELDS
- BOOK - U-LIKE SERIESCHAPTER - ELECTROMAGNETICE INDUCTIONEXERCISE - Self Assessment Test Section -D1videos
ELECTROMAGNETICE INDUCTION
Similar Questions
Which of the following radiation has the least wavelength?
04:24View SolutionIf μ0 be the magnetic permeability are ε0 the electric permittivity of free space then speed of em waves in freee space is given as : c = ______________.
04:24View SolutionSuppose that the electric field part of an electromagnetic wave in vacuum is →E={(3.1N/C)cos[(1.8rad/m)y+(5.4×106rad/s)t]}ˆi.
(a) What is the direction of propagation?
(b) What is the wavelength λ?
(c ) What is the frequency v?
(d) What is the amplitude of the magnetic field part of the wave?
(e) Write an expression for the magnetic field part of the wave.02:01View SolutionThree small , identical point charges lie on the circumference of a circle forming an equilateral triangle.Calculate the value of electric field at the centre of circle.
02:46View Solution(a) Derive the expression for the magnetic energy stored in an inductor when a current I develops in it. Hence, obtain the expression for the magnetic energy density.
(b) A square loop of sides 5 cm carrying a current of 0.2 A in the clockwise direction is placed at a distance of 10 cm from an infinitely long wire carrying a current of 1 A as shown in Fig. 6.66. Calculate (i) the resultant magnetic force, and (ii) the torque, if any, acting on the loop.
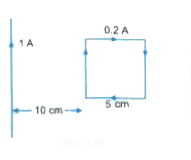 01:47View Solution
01:47View SolutionWhat is intesity of electromagnetic wave? Give its relation in terms of electric field E and magnetic field B
02:44View SolutionWhat is intensityof electromagnetic wave? Give Its relation in terms of electric field E and magnetic field B
03:23View SolutionStatement-1 : A changing electric field produces a magnetic field
Statement-2: A changing magnetic field produces an electric field.View SolutionThe relation between electric field E and magnetic field H in an electromagnetic wave is
View SolutionIf E is an electric field and B is the magnetic induction then the energy flow per unit area per unit time in an electromagnetic field is given by
View SolutionAccording to Maxwell’s hypothesis, a changing electric field gives rise to
View Solution(A ): Induced electric fields are produced by time varying magnetic field. (R): According to faraday’s law ointvecE.vecdl=(dϕ)/(dt)
View Solution(A) : An electric field changing with time gives rise to a magnetic field and vice - versa. (R) : The displacement current is a source of magnetic field.
03:10View SolutionRead the following passage and then answer questions (a) to (e) on the basis of your under- standing of the passage and the related studied concepts. In accordance with Faraday.s law of electromagnetic induction a magnetic field, changing with time, gives rise to an electric field. Again as per Ampere-Maxwell.s law an electric field, changing with time, gives rise to a magnetic field. It means that if we consider a charge oscillating with some frequency, it produces an oscillating electric field in space, which produces an oscillating mag- netic field, which in turn, is a source of oscillating electric field and so on. The oscillating electric and magnetic fields thus regenerate each other and an electromagnetic wave propagates through space. The energy associated with the propagating wave comes at the expense of the energy of the oscillating charge. Electromagnetic wave propagates through free space as a transverse wave in which vecE and vecB are perpendicular to each other as well as perpendicular to the direction of wave propagation. Like other waves electromagnetic waves carry energy and momentum. As electromagnetic waves contains both electric and magnetic fields, it has an electrical energy density mu_(E)=(1)/(2)in_(0)E^(2) as well as a magnetic energy density mu_(B)=(B^(2))/(2mu_(0)). Both of these vary with time. The magnetic field in a plane electromagnetic wave is given by : B_(y)=2xx10^(-7)sin[1.5xx10^(11)t-0.5xx10^(3)x]T What is the speed of electromagnetic wave?
04:02View SolutionRead the following passage and then answer questions (a) to (e) on the basis of your under- standing of the passage and the related studied concepts. In accordance with Faraday.s law of electromagnetic induction a magnetic field, changing with time, gives rise to an electric field. Again as per Ampere-Maxwell.s law an electric field, changing with time, gives rise to a magnetic field. It means that if we consider a charge oscillating with some frequency, it produces an oscillating electric field in space, which produces an oscillating mag- netic field, which in turn, is a source of oscillating electric field and so on. The oscillating electric and magnetic fields thus regenerate each other and an electromagnetic wave propagates through space. The energy associated with the propagating wave comes at the expense of the energy of the oscillating charge. Electromagnetic wave propagates through free space as a transverse wave in which vecE and vecB are perpendicular to each other as well as perpendicular to the direction of wave propagation. Like other waves electromagnetic waves carry energy and momentum. As electromagnetic waves contains both electric and magnetic fields, it has an electrical energy density mu_(E)=(1)/(2)in_(0)E^(2) as well as a magnetic energy density mu_(B)=(B^(2))/(2mu_(0)). Both of these vary with time. What is the frequency and wavelength of the electromagnetic wave?
01:12View Solution

