Refer to figure. Let ΔU1 and ΔU2 be the changes in internal energy of the system in the processes A and B. then
ΔU1>ΔU2
ΔU1=ΔU2
ΔU1<ΔU2
ΔU1≠ΔU2
The correct Answer is:B
To solve the problem, we need to analyze the changes in internal energy (ΔU) during two processes (A and B) that form a cyclic process. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Cyclic Process
The system starts from state 1, undergoes process A to reach state 2, and then undergoes process B to return to state 1. Since the system returns to its initial state, this is a cyclic process.
Hint: Remember that in a cyclic process, the initial and final states are the same.
Step 2: Apply the First Law of Thermodynamics
According to the first law of thermodynamics, the net heat added to the system over a complete cycle is equal to the net work done by the system. Mathematically, this can be expressed as:
∮dQ=∮dW
where the integral is taken over the entire cycle.
Hint: The first law relates heat, work, and internal energy changes.
Step 3: Relate Heat, Work, and Internal Energy
For any thermodynamic process, the first law can be expressed as:
dQ=dU+dW
Integrating this over the entire cycle gives:
∮dQ=∮dU+∮dW
Hint: This equation shows how changes in internal energy relate to heat and work.
Step 4: Analyze the Cyclic Integral
Since the system returns to its initial state, the change in internal energy over the entire cycle is zero:
∮dU=0
This implies that the sum of the changes in internal energy for the two processes (A and B) must also equal zero:
ΔUA+ΔUB=0
Hint: The internal energy change for the entire cycle is zero because the system returns to its original state.
Step 5: Relate Changes in Internal Energy
From the above equation, we can express the change in internal energy for process A (ΔU1) and process B (ΔU2):
ΔU1+ΔU2=0⟹ΔU1=−ΔU2
This means that the change in internal energy during process A is equal in magnitude but opposite in sign to the change in internal energy during process B.
Hint: The negative sign indicates that if one process increases internal energy, the other decreases it by the same amount.
Step 6: Conclusion
Since ΔU1 is equal to -ΔU2, we can conclude that:
ΔU1=ΔU2
This corresponds to option 2 from the question.
Final Answer: The correct option is that ΔU1 is equal to ΔU2.
The system starts from state 1, undergoes process A to reach state 2, and then undergoes process B to return to state 1. Since the system returns to its initial state, this is a cyclic process.
According to the first law of thermodynamics, the net heat added to the system over a complete cycle is equal to the net work done by the system. Mathematically, this can be expressed as:
∮dQ=∮dW
where the integral is taken over the entire cycle.
For any thermodynamic process, the first law can be expressed as:
dQ=dU+dW
Integrating this over the entire cycle gives:
∮dQ=∮dU+∮dW
Since the system returns to its initial state, the change in internal energy over the entire cycle is zero:
∮dU=0
This implies that the sum of the changes in internal energy for the two processes (A and B) must also equal zero:
ΔUA+ΔUB=0
From the above equation, we can express the change in internal energy for process A (ΔU1) and process B (ΔU2):
ΔU1+ΔU2=0⟹ΔU1=−ΔU2
This means that the change in internal energy during process A is equal in magnitude but opposite in sign to the change in internal energy during process B.
Since ΔU1 is equal to -ΔU2, we can conclude that:
ΔU1=ΔU2
This corresponds to option 2 from the question.
Topper's Solved these Questions
Similar Questions
Refer to figure. Let ΔU1 and ΔU2 be the changes in internal energy in the system in process A+B and ΔW be the net work done by the system in the process A+B,

View SolutionA gas is expanded from volume V0=2V0 under three different processes. Process 1 is isobaric process, process 2 is isothermal and process 3 is adiabatic. Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gas in these three processes. then

View Solution
Knowledge Check
A gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gas in these three processes then
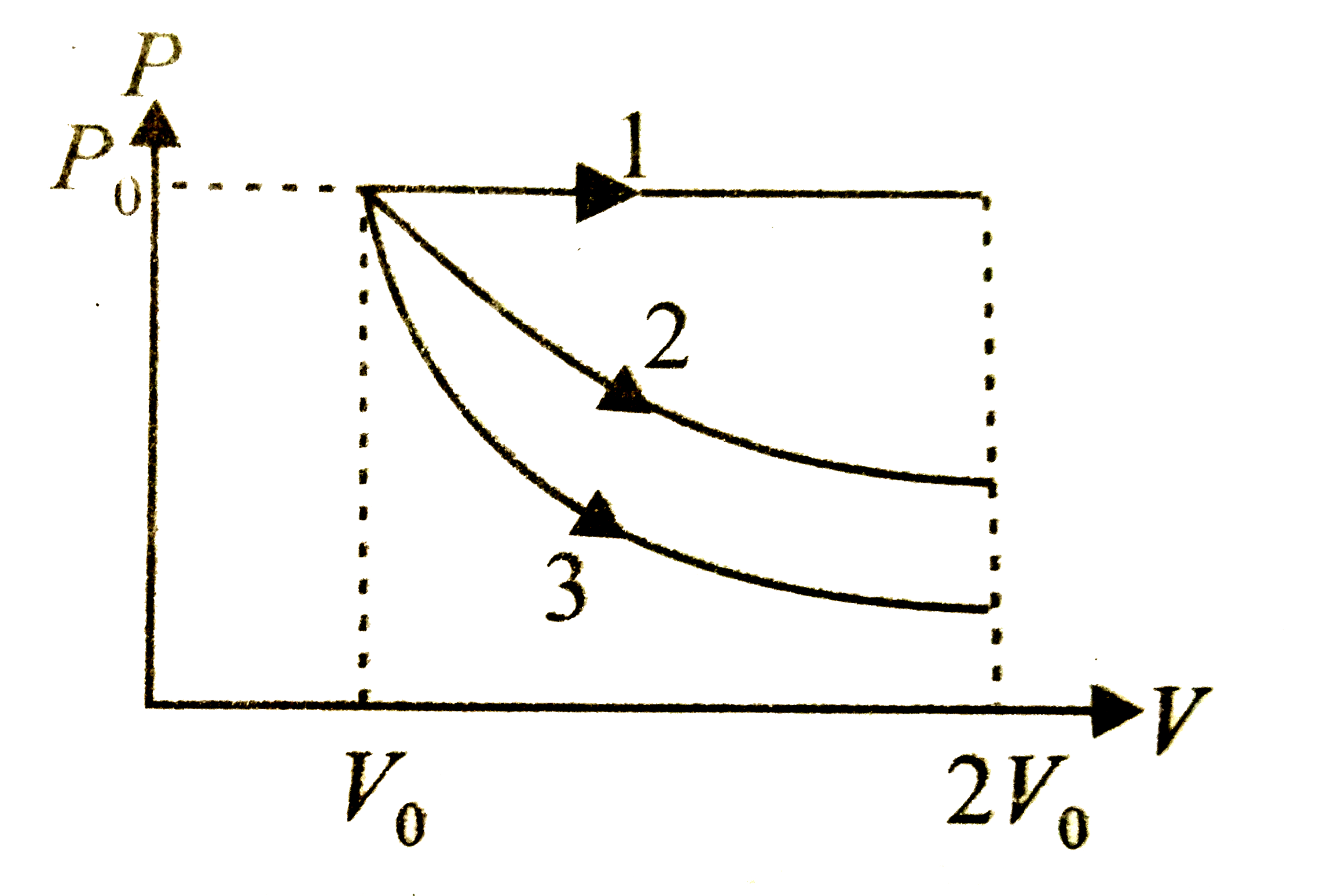 AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3
AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3
A system goes from A and B via two processes. I and II as shown in figure. If ΔU1andΔU2 are the changes in internal energies in the processes I and II respectively, then
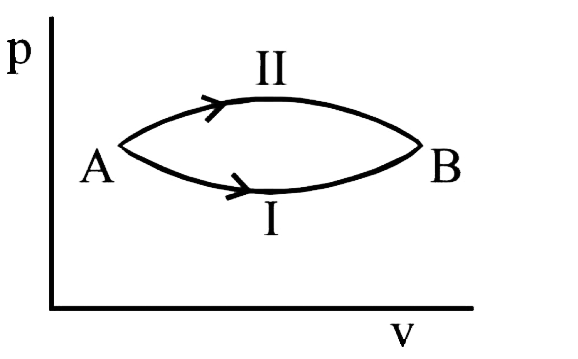
View SolutionA system goes from A and B via two processes. I and II as shown in figure. If ΔU1andΔU2 are the changes in internal energies in the processes I and II respectively, then

View SolutionA system goes from A and B via two processes. I and II as shown in figure. If ΔU1andΔU2 are the changes in internal energies in the processes I and II respectively, then

View SolutionIn given figure, let ΔU1 and ΔU2 be change in internal energy in process ABC and CDA respectively. ΔQ and W be the net heta given and net work done by the system in the process ABC+CDA, then

View SolutionWhat is the change in internal energy of a system undergoing a cyclic process, at the end of a cycle ?
View SolutionConsider two processes on a system as shown in figure.
The volumes in the initial states are the same in the two processes and the volume in the final states are also the same.Let ΔW1 and ΔW2 be the work done by the system in the processes A and B respectively.

View SolutionConsider two processes on a system as shown in figure.
The volumes in the initial states are the same in the two processes and the volume in the final states are also the same.Let ΔW1 and ΔW2 be the work done by the system in the processes A and B respectively.

View Solution
