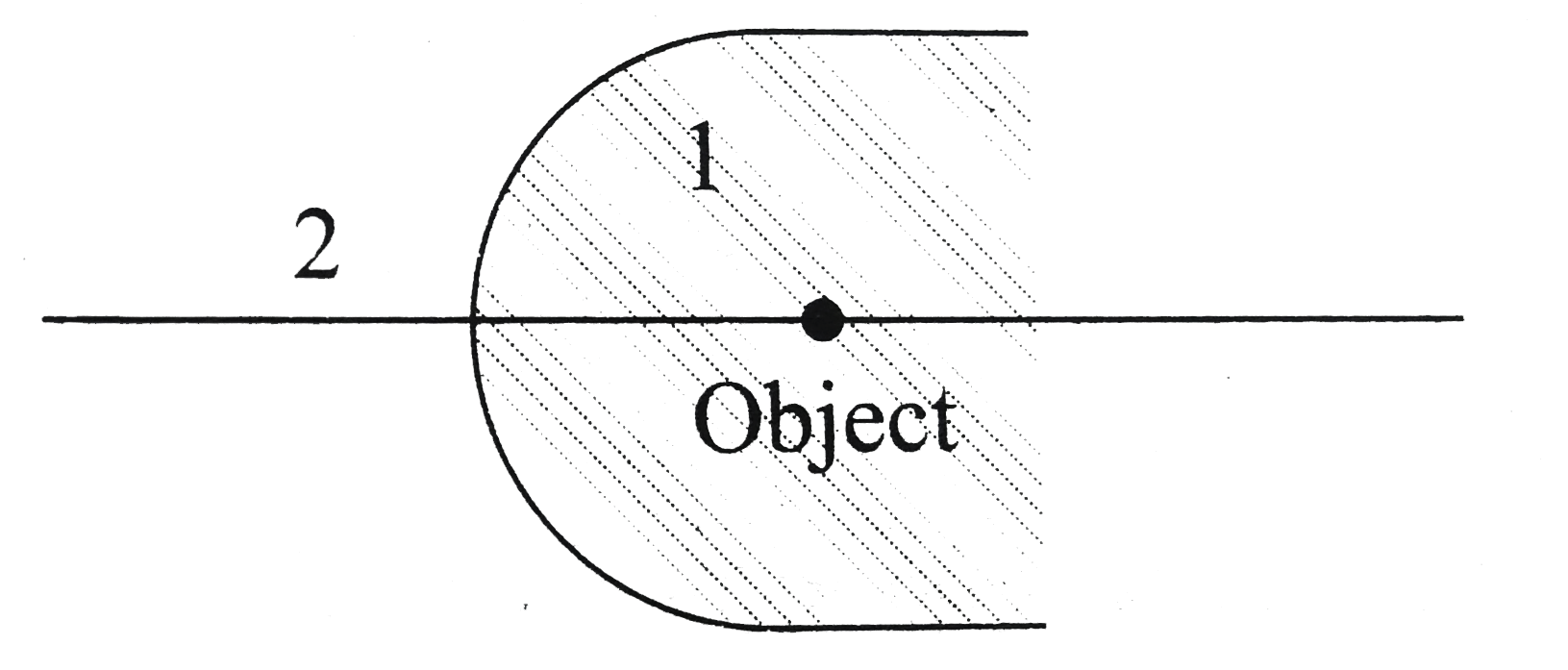
Refraction takes place at a convex spherical boundary separating glass-air medium. For the image to be real, the object distance (μg=3/2) should be /is
greater than three times the radius of curvature of the refracting surface
greater than two times the radius of curvature of the refracting surface
greater than the radius of curvature of the refracting surface
independent of the radius of curvature of the refracting surface
The correct Answer is:a.
Applyingμ2v−μ1u=μ2−μ1R
1v−1.5(−u)=1−(1.5)−R or 1v+32u=12R
For v to be positive, 12R>32u
or u>3R
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
Show that for refraction at a concave spherical surface (separating glass-air medium), the distance of the object should be greater than three times the radius of curvature of the refracting surface for the image to be real.
View Solution(a) A point object is placed on the principal axis of a convex spherical surface of radius of curvature R, which separates the two media of refractive indices nx and n2(n2>n1)
Draw the ray diagram and deduce the relation between the object distance (w), image distance (v) and the radius of curvature (R) for refraction to take place at the convex spherical surface from rarer to denser medium.
(b) A converging lens has a focal length of 20 cm in air. It is made of a material of refractive index 1.6. If it is immersed in a liquid of refractive index 1.3, find its new focal length.
View Solution
Knowledge Check
Refraction takes place at a concave spherical boundary separating glass air medium. For the image to be real, the object distance (μg=3/2)
Ashould be greater than three times the radius of curvature of refracting surfaceBshould be greater than two times the radius of curvature of the refracting surfaceCshould be greater than the radius of curvature of refracting surfaceDis independent of the radius of curvature of the refracting surfaceRefraction takes place at a convex spherical boundary separating air-glass medium. For the image to be real, the object distance (μg=3/2)
Note Object lying in the glass.Ashould be greater than three times the radius of curvature of the refracting surfaceBshould be greater than two times the radius of curvature of the refracting surfaceCshould be greater than the radius of curvature of the refracting surface.Dis independent of the radius of curvature of the refracting surfaceA real object is kept in air and refraction occurs at the convex boundry of a spherical glass surface. For the image to be real, the real object distance (ng=3/2)
AShould be greater than three times the radius of curvature of the refracting surface.BShould be lesser than two times the radius of curvature of the refracting surfaceCShould be greater than the radius of curvature of the refracting surfaceDIs independent of the radius of curvature of the refracting surface
A convex spherical refracting surfaces separates two media glass and air (μg=1.5). If the image is to be real, at what minimum distance u should the object be placed in air if R is the radius of curvature
View SolutionRadius of curvature of a concave spherical surface separating air-glass medium is R. A point object is placed on the principal axis in the glass (mg=1.5). For the image to be real seen by

observer in air, distance of the object from P should be
View SolutionWhere should an object be placed in front of a convex lens to get a real to get real image of the size of the object ?
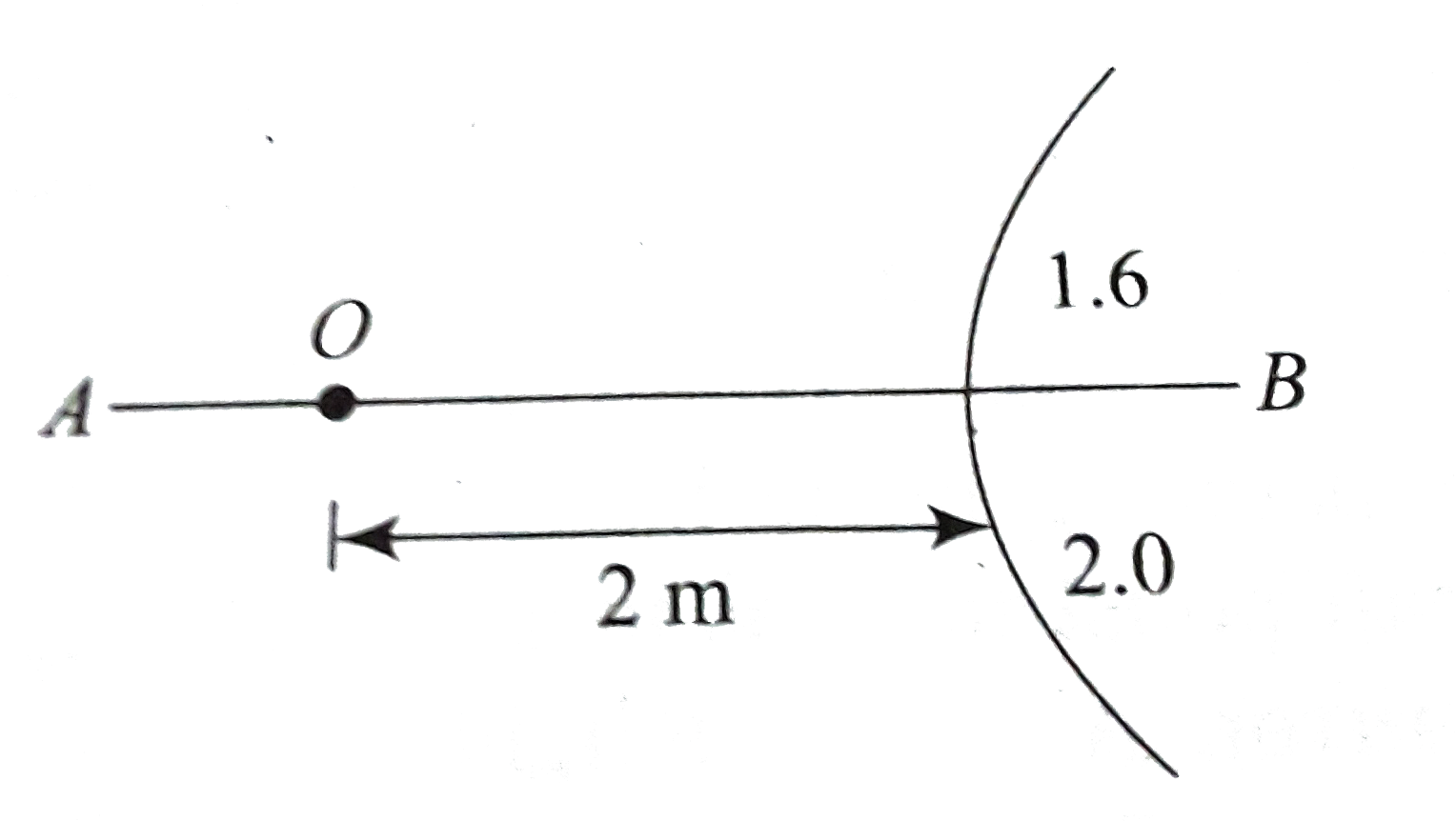
View SolutionIn Figure, a point object O is placed in air. A spherical boundary separates two media. Ab is the principall axis. The refractive index above AB is 1.6 and below AB is 2.0. The separation between the images formed due to refraction at a the spherical surface is (assume the radius of curvature (R) to be 1 unit)
View SolutionThe correct expression for refraction at single convex spherical surface separating two media of refractiv eindices μ1andμ2(μ2>μ1) and radius of curvature R is ( u and v are object, image distane respectively )
View Solution
