Show mathematically that the potential at a point on the equitorial line of an electic dipole is zero.Solution in Punjabi
Electric Potential at any point due to an Electric Dipole : Consider an electric dipole AB having charge - 9 at point A and charge + q at point B and 2a is its dipole length. Let O be the centre of the dipole and P be any point at a distance from its centre, where electric potential due to the dipole is to be determined. Let ∠POB=θ.
The potential at point P due to charge -q,
and the potential at point P due to charge +q,
V2=14π∈0.qPB
Therefore, net potential at point P due to the dipole,
V2=V1+V2=−14π∈0.qPA+14π∈0.qPB
or V=14π∈0.q[1PB−1PA] ......(i)
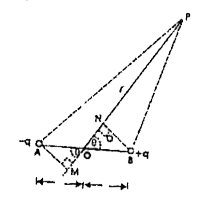
To find PB and PA, draw BN perpendicular to OP and AM perpendicular to PQ after producing it. From right angled AAMO, we have
cosθ=OMOA=OMaorOM=acosθ
In case the length of the dipole is very small as compared to distance r, then PA≈PM=PO+OM=r÷acos
Similarly, it can be obtained that
PB=r−acosθ
In the equation (1), substituting for PA and PB, we have
V=14π∈0.q[1r−acosθ−1r+acosθ]
=14π∈0.q[r+acosθ−r+acosθr2−a2cos2θ]
=14π∈0.q[2acosθr2−a2cos2θ]
Since q (20) = P, the electric dipole moment of the dipole, the above equation becomes
V=14π∈0.Pcosθ(r2−a2cos2θ) ......(2)
The equation (2) gives electric potential due to the dipole at a distance r from its centre in a direction making an angle with the dipole.
Special cases : Let us find the electric potential due to the dipole in the following two cases :
When point P lies on the axial line of the dipole :
In such a case, θ=0∘ and cos0∘=1
Therefore, the equation (2) gives
V=14π∈0.Pcos0∘(r2−a2cos20∘)
V=14π∈0.P(1)(r2−a2)
V=14π∈0.P(r2−a2)
When point P lies on the equitorial line of the dipole :
In such a case, theta=90^(@).andcos90^(@)=0
From equation (2)
y=0
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - NUMERICAL PROBLEMS16videos
ELECTROSTATIC POTENTIAL
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - MOST EXPECTED QUESTIONS7videos
ELECTROSTATIC POTENTIAL
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIALEXERCISE - SHORT ANSWERTYPE QUESTIONS (2 Marks Questions)9videos
ELECTROSTATIC POTENTIAL
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - ELECTRONIC DEVICES SOLIDSEXERCISE - Most Expected Questions9videos
ELECTRONIC DEVICES SOLIDS
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - FORCE ON A CHARGE EXERCISE - NUMERICAL PROBLEMS14videos
FORCE ON A CHARGE
Similar Questions
Two charges 3×10−8Cand−2×10−8C are located 15 cm apart. At what point on the line joining the two charges is the electrical potential zero? Take the potential at infinity to be zero.
08:27View SolutionName the physical quantity whose SI unit is volt metre−1.
View SolutionHow can the whole charge of a conductor be transferred to another isolated conductor?
14:20View SolutionWhy semiconductors are doped?
05:15View SolutionAn electron (with charge 1.6×10−19C) moving at right angles to a uniform magnetic field completes a circular orbit in 10−6sec. Calculate the vlaue of magnetic field. Given mass of electron =9×10−31kg.
53:18View SolutionDerive a relation for electric field of an electric dipole at a point on its equitorial line.
36:00View SolutionShow mathematically that the potential at a point on the equatorial line of an electric dipole is zero.
04:18View SolutionObtain an expression for electric field intensity at any point on equitorial line of electric dipole. What is the direction of electric field?
03:01View SolutionWhat is magnetic dipole? Derive an expression for magnetic field intensity at a point on the equitorial line of a bar magnet.
06:02View SolutionDipole And Dipole Moment|Electric Field At Axial Point Of Dipole|Electric Field At Equitorial Point Of Dipole|Examples
02:41View SolutionPotential Due To Point Charge|Potential Due To System Of Point Charge|Potential At Axial Point Of Dipole |Potential At Equitorial Point Of Dipole
02:41View SolutionIn an electric dipole, at which point is the electric potential zero?
05:15View SolutionElectric potential due to an electric dipole is zero at a point on the………. Line.
05:15View SolutionDefine an electrostatic potential. What are its unit and dimensions ? Show that the potential at a point on the equatorial line of a dipole is zero.
14:20View SolutionWhat is the direction of electric field at a point on the equitorial line of electric dipole ?
View SolutionWhat is the direction of electric field at a point on the equitorial line of electric dipole ?
03:20View Solution

