State and prove De Morgan's Frist and second theorems. Solution in Tamil
The first theorem states that the complement of the sum of two logical inputs is equal to the product of its complements.
Proof :
The Boolean equation for NOR gate is Y=¯¯¯¯¯¯¯¯¯¯¯A+B . The Boolean equation for a bubbled AND gate is Y=¯¯¯A.¯¯¯B . Both cases generate same outputs for same inputs. It can be verified using the following truth table.
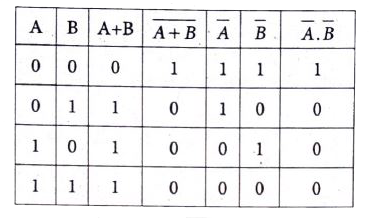
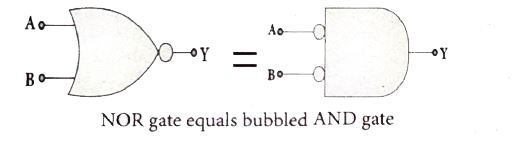
From the above truth table, we can conclude¯¯¯¯¯¯¯¯¯¯¯A+B=¯¯¯A.¯¯¯B . Thus De Morgan’s First Theorem is proved. It also says that a NOR gate is equal to a bubbled AND gate. The corresponding logic circuit diagram is shown in figure.
De Morgan.s Second Theorem:
The second theorem states that the complement of che product of two inputs is equal to the sum of its complements.
Proof:
The Boolean equation for NAND gate is Y=¯¯¯¯¯¯AB.
The Boolean equation for bubbled OR gate is Y=¯¯¯¯¯¯¯¯¯¯¯A+B . A and B are the inputs and Y is the output. The above two equations produces the same output for the same inputs. It can be verified by using the truth table.
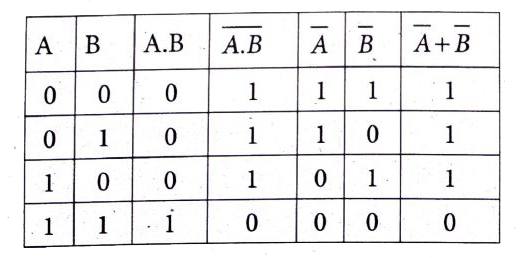
from the above truth table we can conclude ¯¯¯¯¯¯¯¯A.B=¯¯¯A+¯¯¯B. Thus De Morgan’s Second Theorem is proved. It also says, a NAND gate is equal to a bubbled OR gate. The logic circuit diagram is shown in figure.
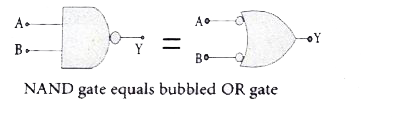
Topper's Solved these Questions
Similar Questions
What are the differences between Coulomb force and gravitational force ?
03:26View SolutionCalculate the electric field due to a dipole on its axial line and equatorial plane.
01:48View SolutionHow do we determine the electric field due to a continuous charge distribution ? Explain. Electric field due to continous charge distribution
07:58View SolutionState De Moivres Theorem and prove it (DeMoivres, DeMoivres Theorem)
03:31View SolutionAccording to de morgan's theorem-
04:34View SolutionState and prove Pythangoras theorem.
08:58View Solutionडी मार्गन नियम (De Morgan's rule ) के लिए बूलियन समीकरण ¯¯¯A⋅¯¯¯B=¯¯¯¯¯¯¯¯¯¯¯A+B से व्यक्त होता है । टूथ टेबुल की सहायता से इस नियम को सिद्ध करे ।
02:56View SolutionState De Morgan's first and second theorems.
04:34View SolutionState and prove De Morgan's Frist and second theorems.
08:58View SolutionState De Morgan's law of sets.
04:34View SolutionState De Morgan's first and second theorems.
07:18View SolutionState and prove De Morgan's Frist and second theorems.
03:33View SolutionState De Morgan's first and second theorems.
05:11View SolutionState and prove Lami's theorem.
02:50View SolutionState and prove a multinomial Theorem.
View Solution

