State Gauss's theorem in electrostatics. Find the electric flux through a surface of area 50m2 in x-y plane in the electric field →E=3ˆi+2ˆj+ˆkV.m−1Solution in Bengali
The unit vector along the normal to the xy plane i.e., z axis is ˆk.
So the area vector =50ˆkm2
∴ Electric flux =∫→E.→ds=∫(3ˆi+2ˆj+ˆk).→ds
=(3ˆi+2ˆj+ˆk).∫→ds=(3ˆi=2ˆj+2ˆk).50ˆk
=50V.m
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE (WBJEE)13videos
ELECTRIC FIELD
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - EXAMINATION ARCHIVE ( JEE MAIN )3videos
ELECTRIC FIELD
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - ENTRACNCE CORNER ( INTEGER ANSWER TYPE )4videos
ELECTRIC FIELD
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - CBSE SCANNER7videos
ELECTRIC ENERGY AND POWER
- BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner13videos
ELECTRIC POTENTIAL
Similar Questions
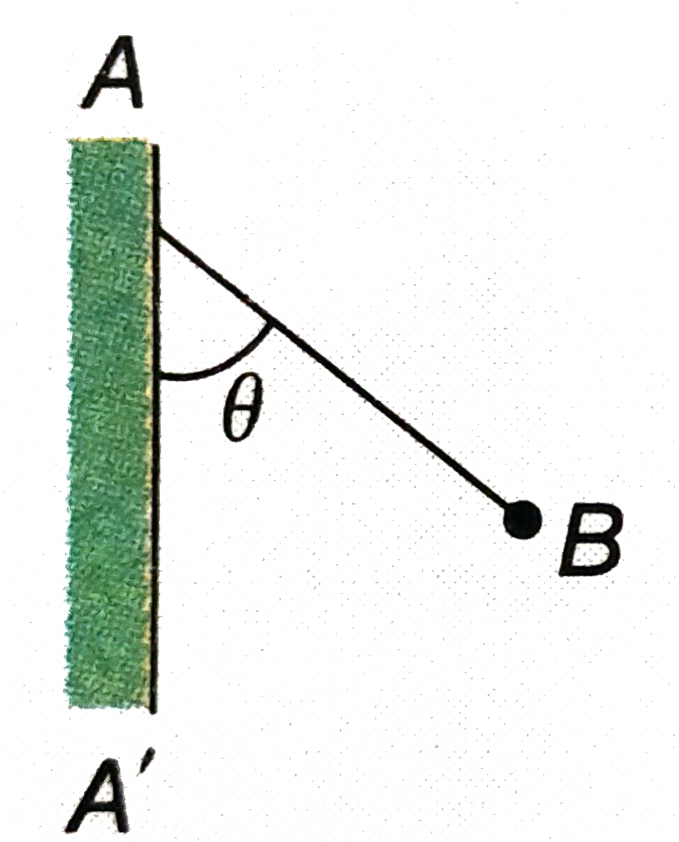
A line AA' is on a charged infinite conducting plane which is perpendicular to the plane of the paper. The plane has a surface density of charge σ and B is a ball of mass m with a like charge of magnitude q.B is connected by a string from a point on the line AA'. The tangent of the angle (θ) formed between the line AA' and the string is
 02:32View Solution
02:32View SolutionA long cylindrical shell carries positive surface charge σ in the upper half and negative surface charge −σ in the lower half. The electric field lines around the cylinder will look like figure given in (figures are schematic and not drawn to scale)
02:00View SolutionTwo charges 2Q and −Q are placed at the points (a,0,0) and (4a,0,0) respectively. With the two charges situated at the cenres, two spheres of radii 2a and 8a are considered. What is the ratio of electric flux through the surfaces of the two spheres?
01:27View SolutionA light bulb is rated 100 W for 220 V ac supply of 50 Hz. Calculate
the resistance of the bulb ,01:25View SolutionA test charge q is moved without acceleration along the path from A to B from B to C in electric field E as shown in fig.

(i) Calculate the potential difference between A and C.01:09View SolutionA hollow half cylinder surface of radius R and length l is placed in a uniform electric field vecE . Electric field is acting perpendicular on the plane ABCD. Find the flux through the curved surface of the hollow cylindrical surface
02:48View SolutionIn a region of space, the electric field is given by →E=8ˆi+4ˆj+3ˆk. The electric flux through a surface of area 100 units in the xy plane is
02:08View SolutionA surface S=10ˆj is kept in an electric field of →E=3ˆi+5ˆj+6ˆk. How much electric flux will come out through the surface?
02:47View SolutionWhat will be the electric flux passing through the area →S=10ˆi placed in an electric field of intensity →E=3ˆi+4ˆj+5ˆk?
03:12View SolutionAn electric is expressed as vecE=20 hatiV.m^(-1) . Find the electric flux passing through a surface of area 0.25m^(2) normal to the x-axis.
View SolutionWhat is the value of electric flux in SI unit in Y-Z plane of area 2m^(2) , if intensity of electric field is vecE=(5hati+2hatj) N//C
02:35View SolutionElectric field intensity in a region of space is given by →E=4ˆi+6ˆj+3ˆk N/C. Consider a plane surface of area 10 units parallel to Y-Z plane and calculate electric flux linked through this surface.
01:35View SolutionWrite the expression for electric flux passing through a surface in the electric field in terms of electric intensity of the field and area of the surface.
04:31View SolutionThe electric field in the region of the space is →E=(5ˆi+2ˆj+3ˆk)NC−1. The electric flux passing through a surface of area 50m2 placed in X-Y plane inside the electric field is.......
04:52View SolutionIt is not convenient to use a spherical Gaussian surface to find the electric field due to an electric dipole using Gauss's theorem because:
02:43View Solution

