Surfaces of a thin equi-convex glass lens have radius of curvature R. Paraxial rays are incident on it . If the final image is formed after n internal reflections, calculate distance of this image from pole of the lens. Refractive index of glass is μ.
The correct Answer is:A, B
To solve the problem, we will follow a systematic approach to calculate the distance of the final image from the pole of a thin equi-convex glass lens after n internal reflections.
1. Identify Given Values:
- Radius of curvature of the lens, R
- Refractive index of glass, μ
- Number of internal reflections, n
2. Refraction at the First Surface:
- For the first refraction, we use the lens maker's formula:
μVi−1∞=μ−1R
- Since rays are coming from infinity, 1∞=0:
μVi=μ−1R
- Rearranging gives:
Vi=μRμ−1
3. Reflection at the First Surface:
- Using the lens formula for the first reflection:
1V1+1Vi=1F
- The focal length F for a thin lens can be approximated as:
F=R2(μ−1)
- Thus, substituting Vi into the lens formula:
1V1+μ−1μR=2(μ−1)R
- Rearranging gives:
1V1=2(μ−1)R−μ−1μR
- Simplifying further leads to:
V1=−3(μ−1)μR
4. Reflection at Subsequent Surfaces:
- For the second reflection, we follow a similar process:
1V2+1V1=1F
- Continuing this process for n reflections, we find:
1Vn=−(2n+1)(μ−1)μR
5. Final Refraction:
- After n reflections, we consider the final refraction:
μVf−1Vn=μ−1R
- Rearranging gives:
Vf=R2μn+μ−1
Final Result:
The distance of the final image from the pole of the lens is:
Vf=R2μn+μ−1
- Radius of curvature of the lens, R
- Refractive index of glass, μ
- Number of internal reflections, n
- For the first refraction, we use the lens maker's formula:
μVi−1∞=μ−1R
- Since rays are coming from infinity, 1∞=0:
μVi=μ−1R
- Rearranging gives:
Vi=μRμ−1
- Using the lens formula for the first reflection:
1V1+1Vi=1F
- The focal length F for a thin lens can be approximated as:
F=R2(μ−1)
- Thus, substituting Vi into the lens formula:
1V1+μ−1μR=2(μ−1)R
- Rearranging gives:
1V1=2(μ−1)R−μ−1μR
- Simplifying further leads to:
V1=−3(μ−1)μR
- For the second reflection, we follow a similar process:
1V2+1V1=1F
- Continuing this process for n reflections, we find:
1Vn=−(2n+1)(μ−1)μR
- After n reflections, we consider the final refraction:
μVf−1Vn=μ−1R
- Rearranging gives:
Vf=R2μn+μ−1
The distance of the final image from the pole of the lens is:
Vf=R2μn+μ−1
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.1
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.2
2 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 11
3 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
If the plane surface of a plano-convex lens of radius of curvature R and refractive index μ is silvered, then its focal length would be
View SolutionPlane surface of a thin plano-convex lens is silvered. If a point object is placed on principal axis at a distance 60cm from the lens and fial image is formed at a distance 30cm from the lens on same side. What will be the distance of final imagge from the lens if the plane surface is not silvered.
View SolutionAn object is at a distance of d=2.5cm from the surface of a glass sphere with a radius R=10cm. Find the position of the final image produced by the sphere. The refractive index of glass is μ=1.5.
View SolutionIn figure , L is half part of an equiconvex glass lens (μ=1.5) whose surfaces have radius of curvature R =40cm and its right surface is silvered . Normal to its principal axis a plane mirror M is placed on right of the lens . Distance between lens L and mirror M is b. A small object O is placed on left of the lens such that there is no parallax between final images formed by the lens and mirror. If transverse length of final image formed by lens is twice that of image formed by the mirror , calculate distance'a' in cm between lens and object.
_S01_072_Q01.png)
View Solution
A point object is placed at a distance R from the convex surface AB of a glass of radius of curvature R1=R and refractive index n=1.5. The second curved surface CD is silvered and its radius of curvature is R2=R if the distance of the final image formed is αR from the surface AB rhen find α?
View Solution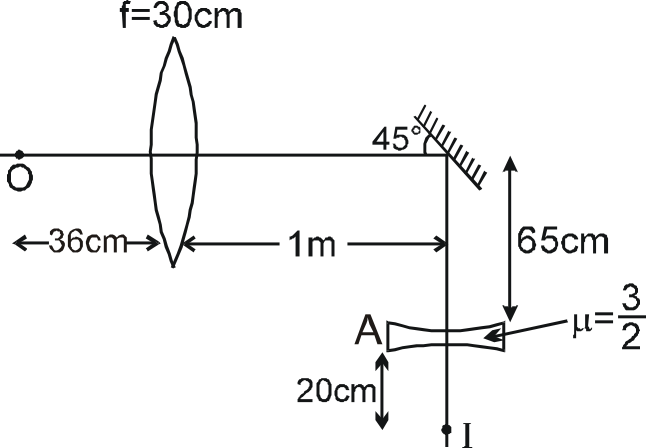
The final image of the object O shown in the figure is formed at point 20 cm below a thin equi-concave lens, which is at a depth of 65 cm from principal axis. From the given geometry, calculate the radius of curvature in cm of lens kept at "A". (Refractive index of equi-convex lens is 1.5 and placed in air.
View Solution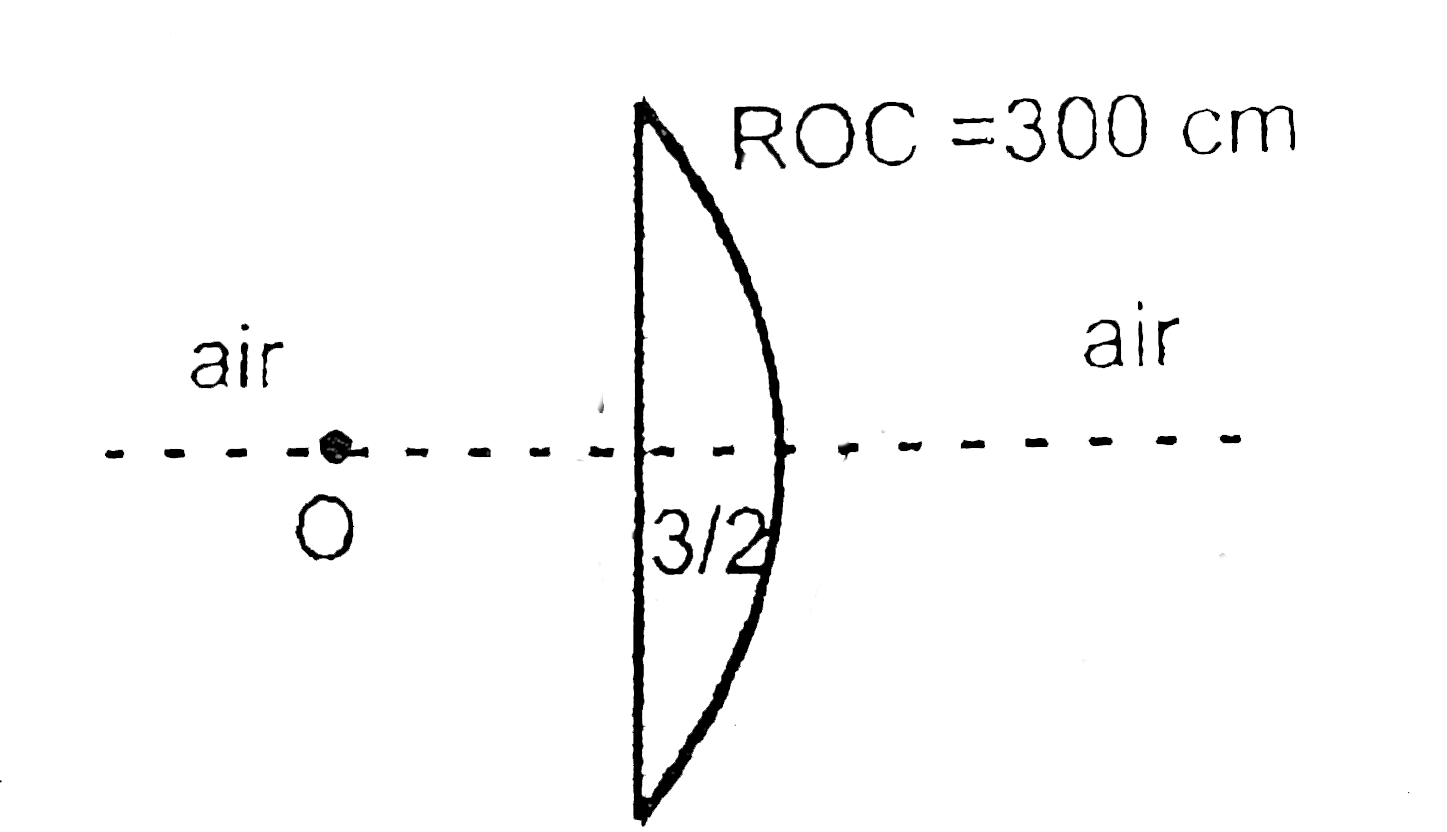
Plane surface of a thin planoconvex lens reflects 50% of light, while the curved surface is completely transparent, if final image of O after refraction through lens coinsides with the image formed due to partial reflection from plane surface. if distance (in m) between O and lens is x then find x/4
View SolutionA point object is placed in front of a silvered plano convex lens of refractive index n radius of curvature R, so that its image is formed on itself. Then the object distance is equal to

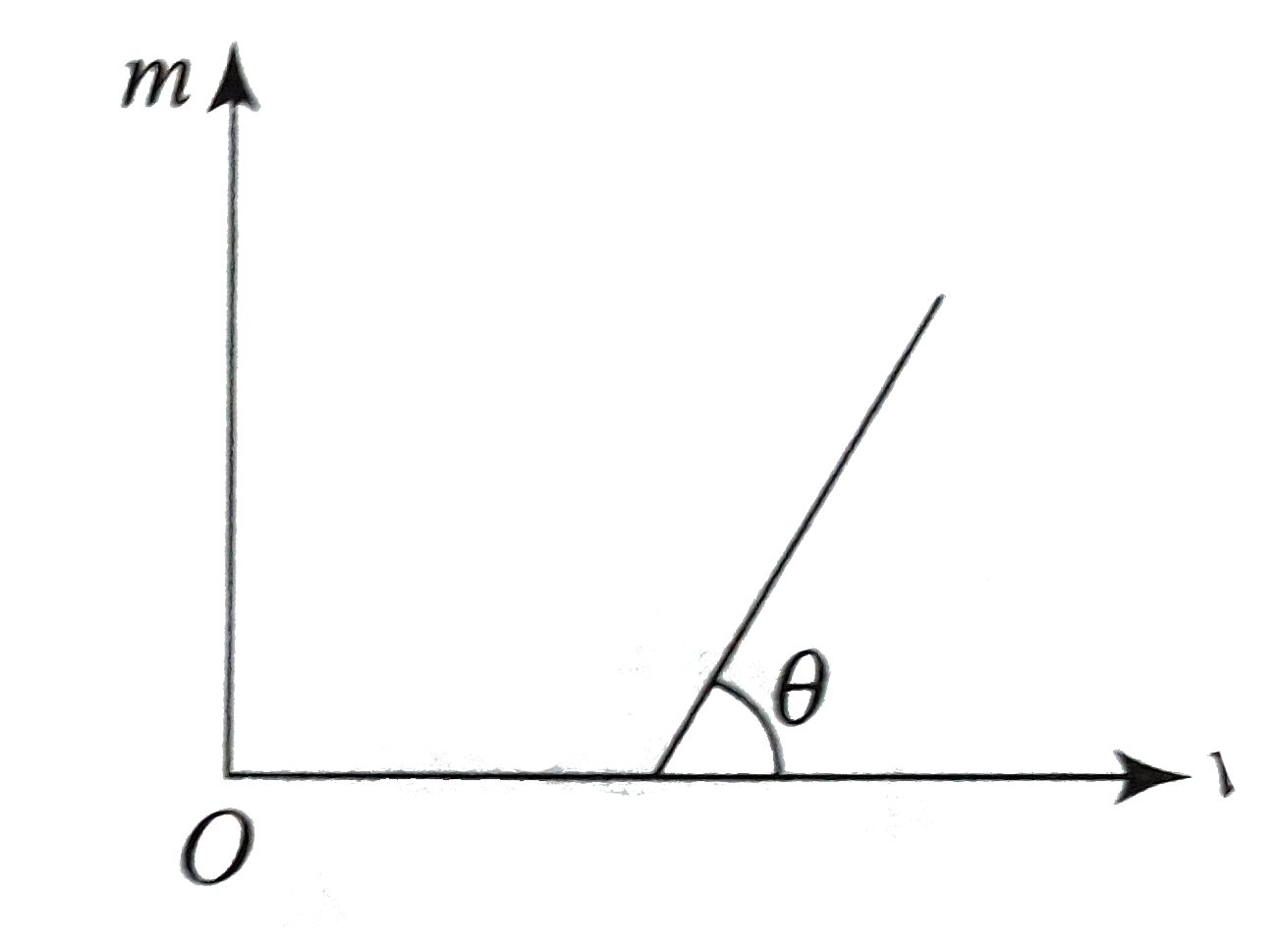
View SolutionFigure, shows variation of magnification m (produced by a thin convex lens) and distance v of image from pole of the lens. When of the following statements are correct?
View Solution
The distance between a convex lens and a plane mirror is 10 cm. The parallel rays incident on the convex lens after reflection from the mirror forms image at the optical centre of the lens. Focal length of lens will be
View Solution
