The angular velocity of a particle moving in a circle of radius 50cm is increased in 5 min from 100 revolutions per minute to 400 revolutions per minute. Find the tangential acceleration of the particle.
60ms−2
π/30ms−2
π/15ms−2
π/60ms−2
The correct Answer is:D
(d) ∝=(ω2−ω1)/t=(400−100)/5=60rev−2min
=60×2π((60))2=2π60rads−2
at=∝r=2π60×50100=π60ms−2.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Multiple Correct11videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Assertion - Reasoning5videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Subjective40videos
KINEMATICS-2
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer9videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression2videos
KINETIC THEORY OF GASES
Similar Questions
A particle is moving in a circle of radius 100 cm making 200 revolutions per minute . After 10 minutes , the revolutions per minute are increased to 300. Calculate angular acceleration and linear acceleration.
View SolutionFigure shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5 m at a given instant of time. At this instant, Find: (i) the radial acceleration, (ii) the speed of the particle and (iii) its tangential acceleration.
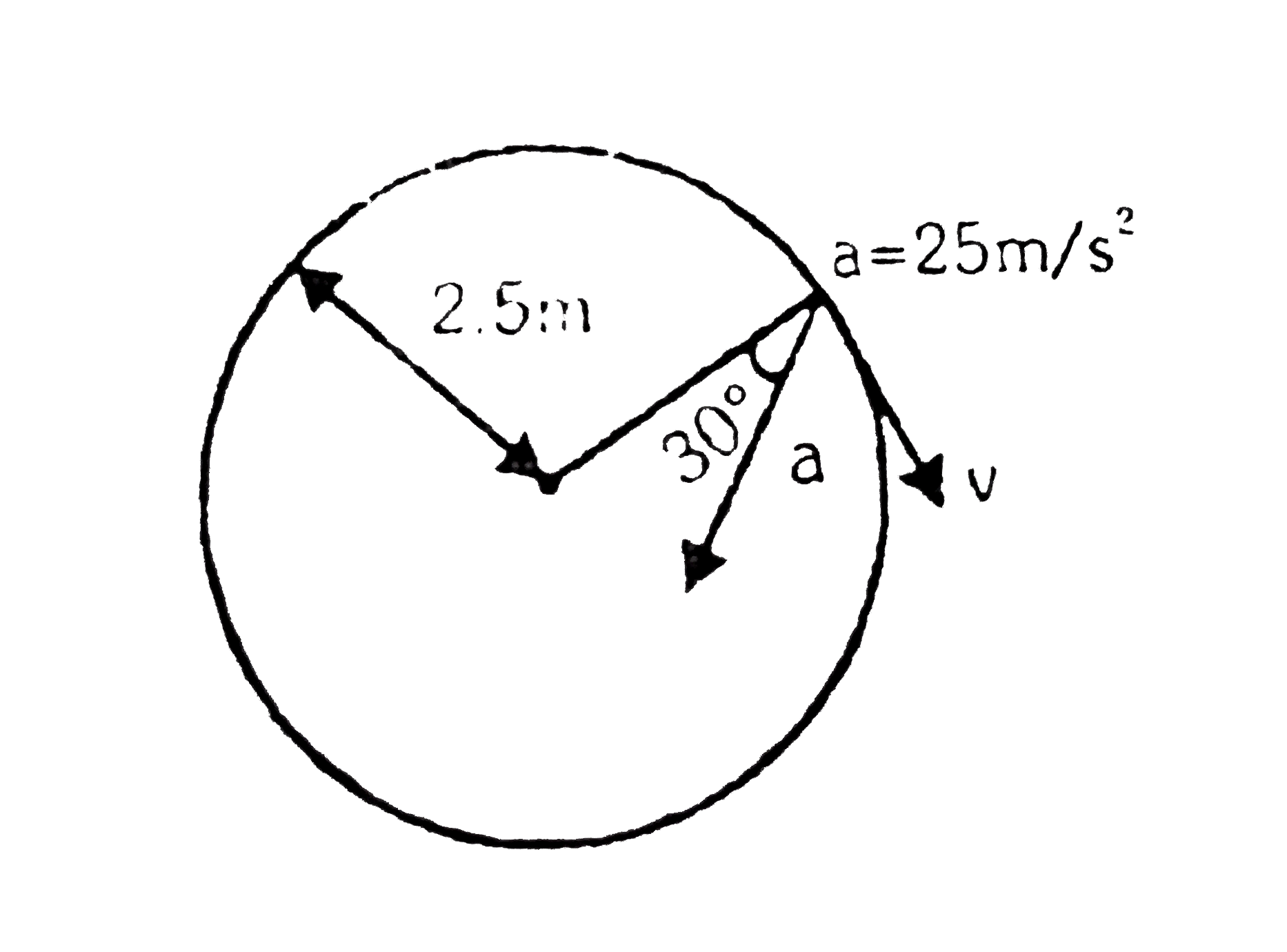 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The angular velocity of a particle rotating in a circular orbit 100 times per minute is
A1.66rad/sB10.47rad/sC10.47deg/sD60deg/s - Question 2 - Select One
The angular speed of a particle,moving in a circle of radius 20 cm ,increases from 2rad/s→40rad/s in 19 s the ratio of its centripetal acceleration to tangential acceleration at the end of 19 s is ,
A400:1B1:800C1:400D800:1 - Question 3 - Select One
A particle moves in a circle of radius 20 cm with linear speed of 10 m/s. Find the angular velocity
A500radsB150radsC50radsD15rads
Figur shows the total acceleration and velocity of a particle moving clockwise in a circle of radius 2.5m at a given instant of time. At this instant, find:
(a) the radius acceleration,
(b) the speed of the acceleration,
(c) its tangential acceleration.
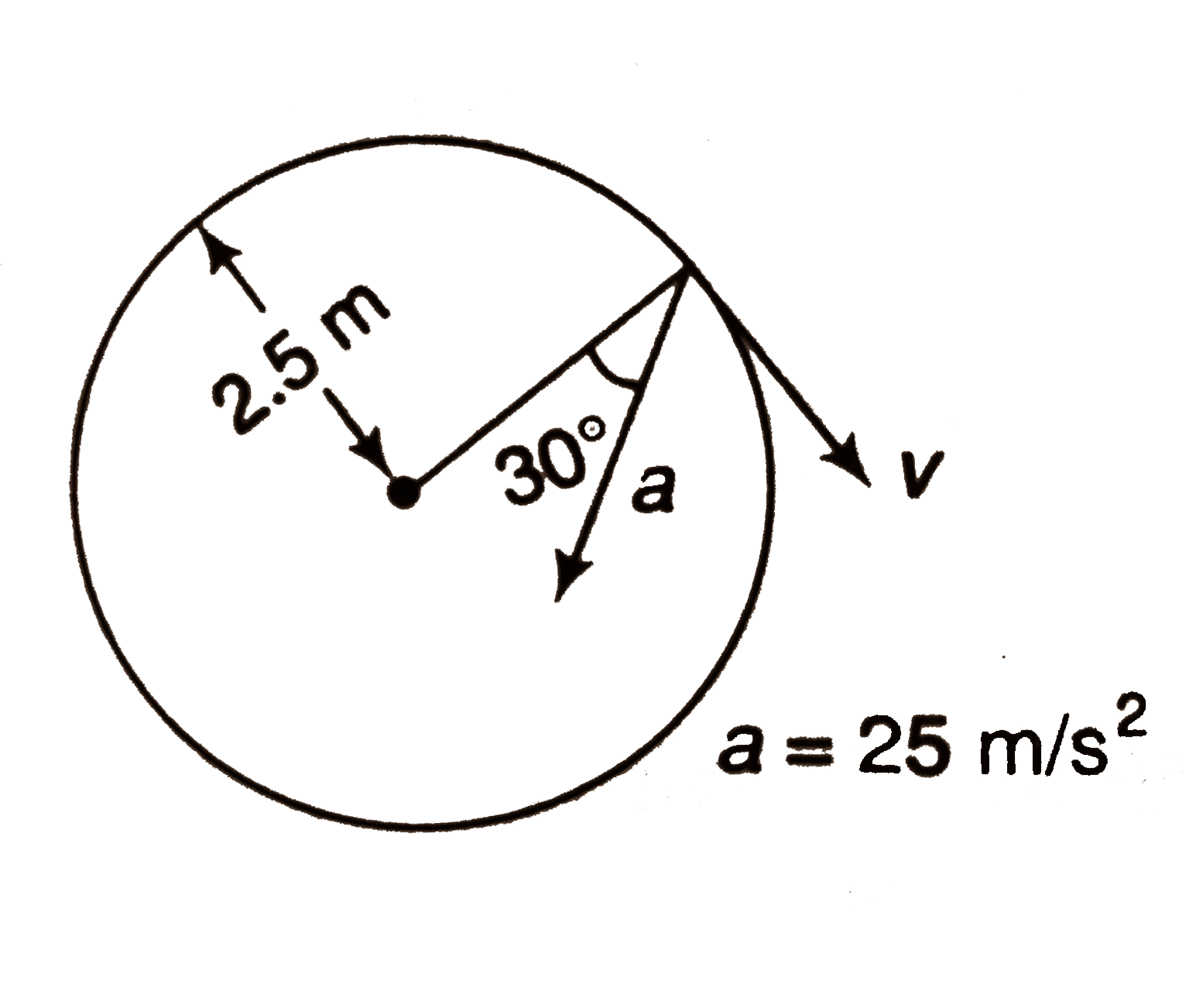 View Solution
View SolutionA particle is moving in a circle of radius 1.5 m. Its speed is increasing by 180 rev/ minute in one mintue , what is its linear acceleration ?
View SolutionA particle moves along a circle of radius (20π) metre with constant tangential acceleration .If the velocity of the particle is 40 m/s at the end of second revolution , after the revolution has began , then the tangential acceleration .If the velocity of the particle is 40 m/s at the end of second revolution , after the revolution has began , then the tangential acceleration is
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period 0.2πs. The acceleration of the particle is
View SolutionA particle moves in a circle of radius 5 cm with constant speed and time period 0.2π. The acceleration of the particle is:
View Solution

