The bob of a simple pendulum is displaced from its equilibrium position 'O' to a position 'Q' which is at a height 'h' above 'O' and the bob is then released. Assuming the mass of the bob to be 'm' and time period of oscillation to be 2.0s, the tension in the string when the bob passes through 'O' is
m(g+π√2gh)
m(g+√π2gh)
m(g+√π22gh)
m(g+√π23gh)
The correct Answer is:A
To find the tension in the string when the bob of a simple pendulum passes through the equilibrium position 'O', we can follow these steps:
Step 1: Understand the Forces Acting on the Bob
At the equilibrium position 'O', two forces act on the bob:
1. The gravitational force (weight) acting downward: Fg=mg
2. The tension in the string acting upward: T
Step 2: Apply Newton's Second Law
When the bob passes through point 'O', it is moving with a certain velocity. According to Newton's second law, the net force acting on the bob is equal to the mass of the bob times its acceleration. The centripetal acceleration is provided by the tension in the string minus the weight of the bob.
The equation can be written as:
T−mg=mv2r
Where:
- T is the tension in the string
- mg is the weight of the bob
- mv2r is the centripetal force required to keep the bob moving in a circular path
Step 3: Solve for Tension
Rearranging the equation gives:
T=mg+mv2r
Step 4: Find the Velocity v
To find v, we can use the conservation of energy principle. When the bob is at the height h (position 'Q'), all the energy is potential energy, and when it passes through 'O', all the potential energy converts into kinetic energy.
The potential energy at height h is:
PE=mgh
The kinetic energy at point 'O' is:
KE=12mv2
Setting the potential energy equal to the kinetic energy gives:
mgh=12mv2
Cancelling m from both sides (assuming m≠0):
gh=12v2⟹v2=2gh
Step 5: Find the Angular Frequency ω
The angular frequency ω can be calculated using the time period T:
ω=2πT
Given that the time period T=2.0s:
ω=2π2=πrad/s
Step 6: Substitute v2 into the Tension Equation
Now substituting v2=2gh into the tension equation:
T=mg+m(2gh)r
Step 7: Final Expression for Tension
Substituting v2 into the tension equation gives:
T=mg+m(2gh)r
This can be simplified to:
T=mg+2mg=3mg
Conclusion
Thus, the tension in the string when the bob passes through point 'O' is:
T=3mg
At the equilibrium position 'O', two forces act on the bob:
1. The gravitational force (weight) acting downward: Fg=mg
2. The tension in the string acting upward: T
When the bob passes through point 'O', it is moving with a certain velocity. According to Newton's second law, the net force acting on the bob is equal to the mass of the bob times its acceleration. The centripetal acceleration is provided by the tension in the string minus the weight of the bob.
T−mg=mv2r
Where:
- T is the tension in the string
- mg is the weight of the bob
- mv2r is the centripetal force required to keep the bob moving in a circular path
Rearranging the equation gives:
T=mg+mv2r
To find v, we can use the conservation of energy principle. When the bob is at the height h (position 'Q'), all the energy is potential energy, and when it passes through 'O', all the potential energy converts into kinetic energy.
PE=mgh
The kinetic energy at point 'O' is:
KE=12mv2
mgh=12mv2
Cancelling m from both sides (assuming m≠0):
gh=12v2⟹v2=2gh
The angular frequency ω can be calculated using the time period T:
ω=2πT
Given that the time period T=2.0s:
ω=2π2=πrad/s
Now substituting v2=2gh into the tension equation:
T=mg+m(2gh)r
Substituting v2 into the tension equation gives:
T=mg+m(2gh)r
This can be simplified to:
T=mg+2mg=3mg
Thus, the tension in the string when the bob passes through point 'O' is:
T=3mg
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective type
3 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A simple pendulum of length l and bob of mass m is displaced from its equilibrium position O to a position P so that hight of P above O is h . If is then released. What is the tension in the string when the bob passes through the through the equilibrium position O ? Neglect friction. v is the velocity of the bob at O
View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionSuppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
View SolutionA simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
View SolutionThe bob of a simple pendulum of length /has a positive charge q on it. The pendulum is fixed to a horizontally oriented positively charged sheet as shown in the figure. The time period of the small oscillations of simple pendulum is
View SolutionThe free end of a simple pendulum is attached to the ceiling of a box. The box is taken to a height and the pendulum is oscillated. When the bob is at its lowest point the box is released to fall freely. As seen from the box during this period the bob will
View SolutionIf the inertial mass m1 of the bob of a simple pendulum of length 'l' is not equal to the gravitationalmassmg, then its period is
View SolutionThe bob A of a simple pendulum is released when the string makes an angle of 45∘ with the vertical. It hits another bob B of the same material and same mass kept at rest on the table. If the collision is elastic, then

View SolutionThe figure below shows a simple pendulum of mass 200 g. It is displaced from the mean position A to the extreme position B. The potential energy at the position A is zero. At the position B the pendulum bob is raised by 5 m.
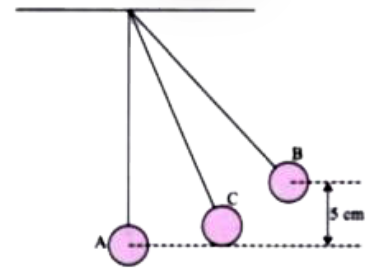
(i) What is the potential energy of the pendulum at the position B?
(ii) What is the total mechanical energy at point C?
(iii) What is the speed of the bob at the position A when released from B ?
(Take g = 10ms−2 and there is no loss of energy.)
View SolutionThe bob A of a simple pendulum is released from a horizontal position A as shownin in figure. If the length of the pendulum is 1.5m , what is the speed with which the bob arrives at the lowermost point B, given that it dissipates 5% of its initial energy against air resistance ?
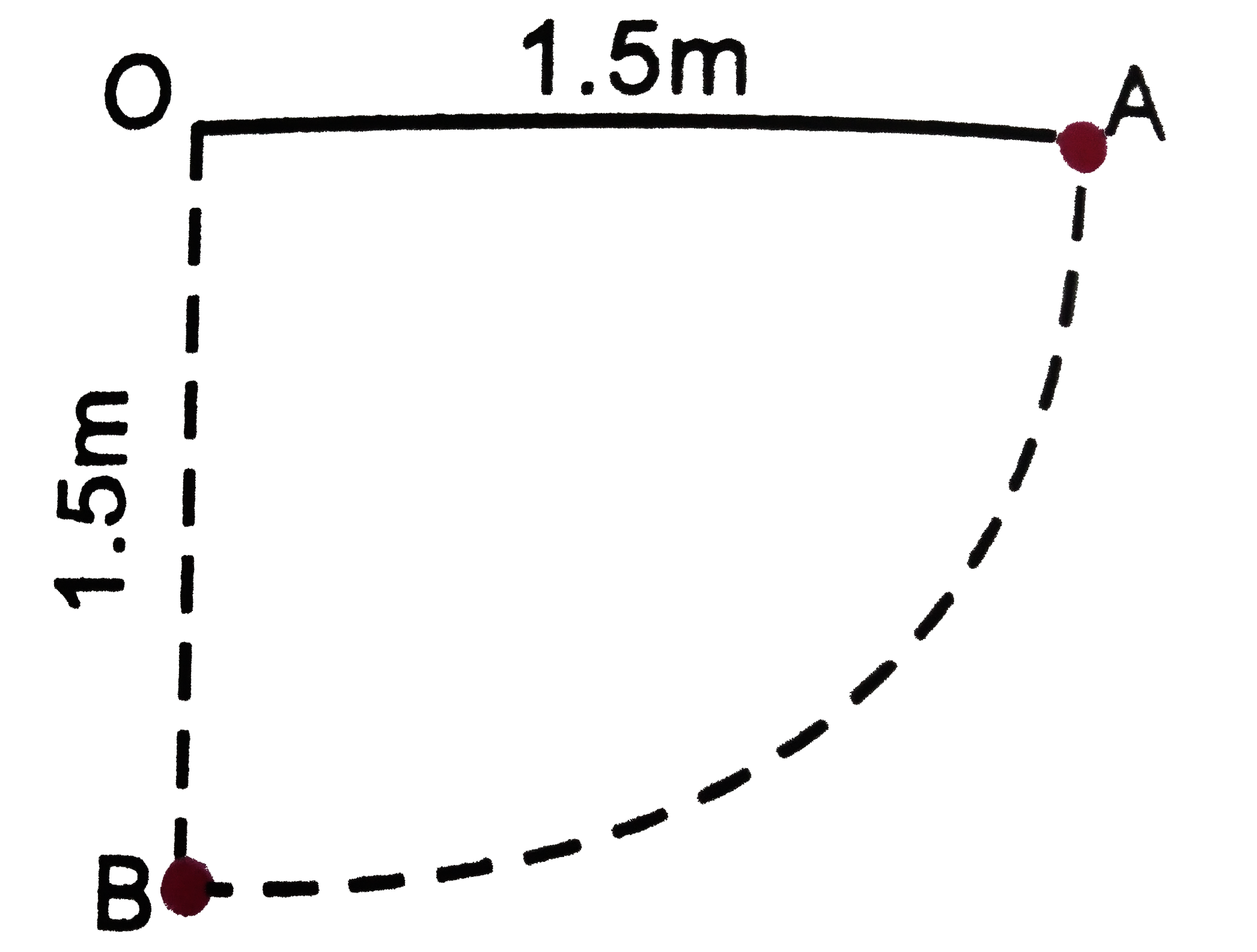
View Solution
