The component of a vector r along X-axis will have maximum value if :
r is along positive Y-axis
r is along positive X-axis
r makes an angle of 45∘ with the Y-axis
r is along regative Y-axis
To determine when the component of a vector r along the X-axis will have its maximum value, we can follow these steps:
Step 1: Understand the Vector Components
A vector r can be represented in terms of its components along the X and Y axes. The component of the vector r along the X-axis can be expressed as:
rx=|r|cos(θ)
where |r| is the magnitude of the vector and θ is the angle the vector makes with the positive X-axis.
Step 2: Analyze the Cosine Function
The cosine function cos(θ) reaches its maximum value of 1 when θ=0∘. This means that the component rx will be maximum when the angle θ is zero.
Step 3: Determine the Condition for Maximum Component
From the above analysis, we conclude that:
- The component rx is maximum when θ=0∘, which means the vector r is aligned along the positive X-axis.
Step 4: Evaluate the Given Options
Now, we evaluate the options provided in the question:
1. r is along the positive Y-axis - Incorrect (this would make rx=0).
2. r is along the positive X-axis - Correct (this gives rx=|r|).
3. r makes an angle of 45 degrees with the Y-axis - Incorrect (this would give a reduced value of rx).
4. r is along the negative Y-axis - Incorrect (this would also make rx=0).
Conclusion
Thus, the component of the vector r along the X-axis will have a maximum value when r is along the positive X-axis.
Final Answer
The correct option is: r is along the positive X-axis.
---
A vector r can be represented in terms of its components along the X and Y axes. The component of the vector r along the X-axis can be expressed as:
rx=|r|cos(θ)
where |r| is the magnitude of the vector and θ is the angle the vector makes with the positive X-axis.
The cosine function cos(θ) reaches its maximum value of 1 when θ=0∘. This means that the component rx will be maximum when the angle θ is zero.
From the above analysis, we conclude that:
- The component rx is maximum when θ=0∘, which means the vector r is aligned along the positive X-axis.
Now, we evaluate the options provided in the question:
1. r is along the positive Y-axis - Incorrect (this would make rx=0).
2. r is along the positive X-axis - Correct (this gives rx=|r|).
3. r makes an angle of 45 degrees with the Y-axis - Incorrect (this would give a reduced value of rx).
4. r is along the negative Y-axis - Incorrect (this would also make rx=0).
Thus, the component of the vector r along the X-axis will have a maximum value when r is along the positive X-axis.
The correct option is: r is along the positive X-axis.
Topper's Solved these Questions
- SELF ASSESSMENT PAPER 02BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 02EXERCISE - SECTION - A(Answer the following )
7 Videos
- SELF ASSESSMENT PAPER 02BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 02EXERCISE - SECTION-B (Answer the following )
13 Videos
- SELF ASSESSMENT PAPER 01BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 01EXERCISE - SECION- D (Answer the following )
6 Videos
- SELF ASSESSMENT PAPER 3BOOK - ICSECHAPTER - SELF ASSESSMENT PAPER 3EXERCISE - Section-D
6 Videos
Similar Questions
The component of a vector →A along y-axis will have maximum value if
View SolutionThe component of a vector is
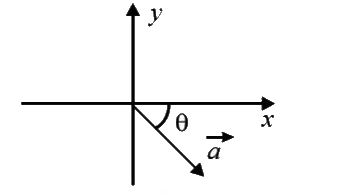
View SolutionWhat is the component of the vector →a along the x-axis in the situation shown in figure ? |→a|=5 units.
View SolutionThe x and Y components of a vector ¯¯¯P have numerical values 5 and 6 respectively. Find the vector ¯¯¯P
View SolutionSuppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is
View SolutionThe x and y components of a position vector P have numerical values 5 and 6 respectively. Direction and magnitude of vector P are
View SolutionThe components of a vector →a along and perpendicular to a non-zero vector →b are ________ and ___________, respectively.
View SolutionThe components of a vector along the x- and y- directions are (n+1) and 1, respectively. If the coordinate system is rotated by an angle θ=60∘, then the components change to n and 3. The value of n is
View SolutionFind component of vector A +B along (i) x-axis, (ii) C. Given A=ˆi−2ˆj,B=2ˆi+3ˆk and C=ˆi+ˆj.
View SolutionFind component of vector A +B along (i) x-axis, (ii) C. Given A=ˆi−2ˆj,B=2ˆi+3ˆk and C=ˆi+ˆj.
View Solution
