The count rate from 100 cm3 of a radioactive liquid is c.Some of this liquid is now discarded. The count rate of the remaining liquid is found to be c/10 after three half-lives. The volume of the remaining liquid, in cm3 , is
Initial count rate (CR) for 1 cm3 of liquid =c100
After 3 half - lives , CR for 1 cm3 of liquid =18×c100
Let the volume of the remaining liquid =Vcm3
CR of this liquid =V×c800=c10 or V=80
Similar Questions
10dm3 of a liquid A was mixed with 10dm3 of liquid B . The volume of the resulting solutino was found to be 19dm3. What do you conclude ?
View SolutionA liquid can rise to a height of h in a capillary tube of length l (l>h). The tube filled with the liquid is kept horizontal with its two ends open. Now the tube is kept vertical with the liquid in it. Some liquid flows out. Find the height of the liquid remaining in the tube if the surface tension of the liquid is σ.
View Solution
Knowledge Check
- Question 1 - Select One
The count rate of a radioactive sample falls from 4.0×106s−1 to 1.0×106s−1 in 20 hours. What will be the count rate after 100 hours from beginning ?
A3.91×103s−1B3.91×102s−1C3.91×104s−1D3.91×106s−1
A liquid at 30°C is poured verly slowly into a Calorimeter that is at temperature of 110°C. The boiling temperature of the liquid is 80°C. It is found that the first 5 gm of the liquid completely evaporates. After pouring another 80 gm of the liquid the equilibrium temperature is found to be 50°C. The ratio of the Latent heat of the liquid to its specific heat will be ____C°.
[Neglect the heat exchange with surrounding.]View SolutionA convex lens is held 45cm above the bottom of an empty tank. The image of a point at the bottom of a tank is formed 36cm above the lens. Now, a liquid is poured into the tank to a depth of 40cm. It is found that the distance of the image of the same point on the bottom of the tank is 48cm above the lens. Find the refractive index of the liquid.
View SolutionWhen a long capillary tube of radius 0.015 cm is dipped in a liquid, the liquid rises to a height of 15 cm within it. If the contact angle between the liquid and glass to close to 0∘, the surface tension of the liquid, in milliNewton m−1, is [ρliquid=900kgm−3,g=10ms−2] (give anwer is closet integer)
View SolutionIn the radioactive decay of an element it is found that the count rate reduces from 1024 to 128 in 3 minutes. Its half life will be
View SolutionA uniform solid cylinder of density 0.8g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are 0.7g/cm3 and 1.2g/cm3, respectively. The height of liquid A is hA=1.2cm. The length of the part of the cylinder immersed in liquid B is hB=0.8cm.
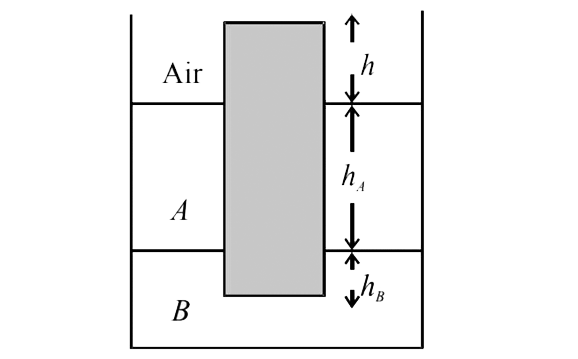
(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.View SolutionA uniform solid cylinder of density 0.8g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are 0.7g/cm3 and 1.2g/cm3, respectively. The height of liquid A is hA=1.2cm. The length of the part of the cylinder immersed in liquid B is hB=0.8cm.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.View SolutionA uniform solid cylinder of density 0.8g/cm3 floats in equilibrium in a combination of two non-mixing liquids A and B with its axis vertical.
The densities of the liquids A and B are 0.7g/cm3 and 1.2g/cm3, respectively. The height of liquid A is hA=1.2cm. The length of the part of the cylinder immersed in liquid B is hB=0.8cm.

(a) Find the total force exerted by liquid A on the cylinder.
(b) Find h, the length of the part of the cylinder in air.
(c) The cylinder is depressed in such a way that its top surface is just below the upper surface of liquid A and is then released. Find the acceleration of the cylinder immediately after it is released.View Solution

