The diagram below shows an image formed at a distance 36 cm from the lens LL' of focal length 12 cm. With respect to this answer the questions that follow.
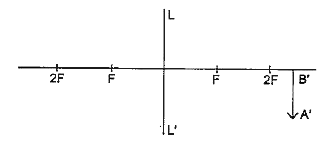
The diagram below shows an image formed at a distance 36 cm from the lens LL' of focal length 12 cm. With respect to this answer the questions that follow. The position of the object on the left-hand side should be:
The position of the object on the left-hand side should be:

A

between 12 cm to 30 cm from the lens.

B

beyond 24 cm from the lens.

C

between 12 cm to 24 cm from the lens.

D

within 12 cm from the lens.

Text Solution
Verified by Experts

The correct Answer is:C

Explanation: As an real and inverted image formed so the lens will be convex
Given: v = 36 cm , f = 12 cm
By 1 f = 1 v - 1 u
1 u = 1 v - 1 f = 1 36 - 1 12
= 1 - 3 36 = - 2 36 = - 1 18
u = - 18 cm

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 10PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The diagram below shows an image formed at a distance 36 cm from the lens LL' of focal length 12 cm. With respect to this answer the questions that follow.
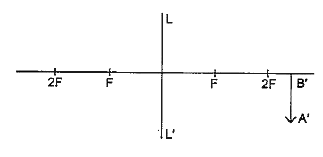
    ocr_image
    Power of this lens is:

    A−8.33 D
    B+8.4 D
    C+8.33 D
    D−8.4 D

  • The diagram below shows an image formed at a distance 36 cm from the lens LL' of focal length 12 cm. With respect to this answer the questions that follow.
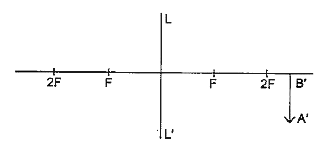
    ocr_image
    The object distance with sign convention is:

    A−18 cm
    B−15 cm
    C−9 cm
    D+18 cm

  • The diagram below shows an image formed at a distance 36 cm from the lens LL' of focal length 12 cm. With respect to this answer the questions that follow.
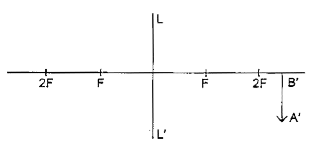
    ocr_image
    If the lens LL'. is replaced by another lens of same type but focal length 15 cm then for the same object distance.

    Athe size of the image decreases.
    Bthe size of the image increases.
    Cthe size of the image remains the same.
    Dinformation is insufficient to conclude.