The distance traversed by a particle moving along a straight lne is given by x=180t+50t2 metre. The acceleration of the particle is
180ms−2
580ms−2
100ms−2
50ms−2
The correct Answer is:C
x=180t+50t2
υ=dxdt=180+100t
a=dυdt=100m/s2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.415videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.525videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.210videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
The displacement x of a particle at time t along a straight line is given by x=α−βt+γt2. The acceleraion of the particle is
View SolutionThe displacement x of a particle along a straight line at time t is given by x=a0+a1t+a2t2. The acceleration of the particle is
View SolutionThe displacement (in metre) of a particle moving along X-axis is given by x=18t+5t2. The average acceleration during the interval t1=2s and t2=4s is
View SolutionThe speed v of a particle moving along a straight line is given by a+bv2=x2 where x is its distance from the origin. The acceleration of the particle is
View SolutionKinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionThe displacement (in metre) of a particle moving along x-axis is given by x=18t+5t2 Calculate (i) instantaneous acceleration.
View SolutionThe displacement of a particle moving along the x-axis is given by equation x=2t3−21t2+60t+6.The possible acceleration of the particle when its velocity is zero is
View SolutionThe acceleration of a particle moving along a straight line at any time t is given by a = 4 - 2v, where v is the speed of particle at any time t The maximum velocity is
View SolutionThe displacement x of a particle along the x-axis at time t is given by x=a12t+a23t2. Find the acceleration of the particle.
View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−
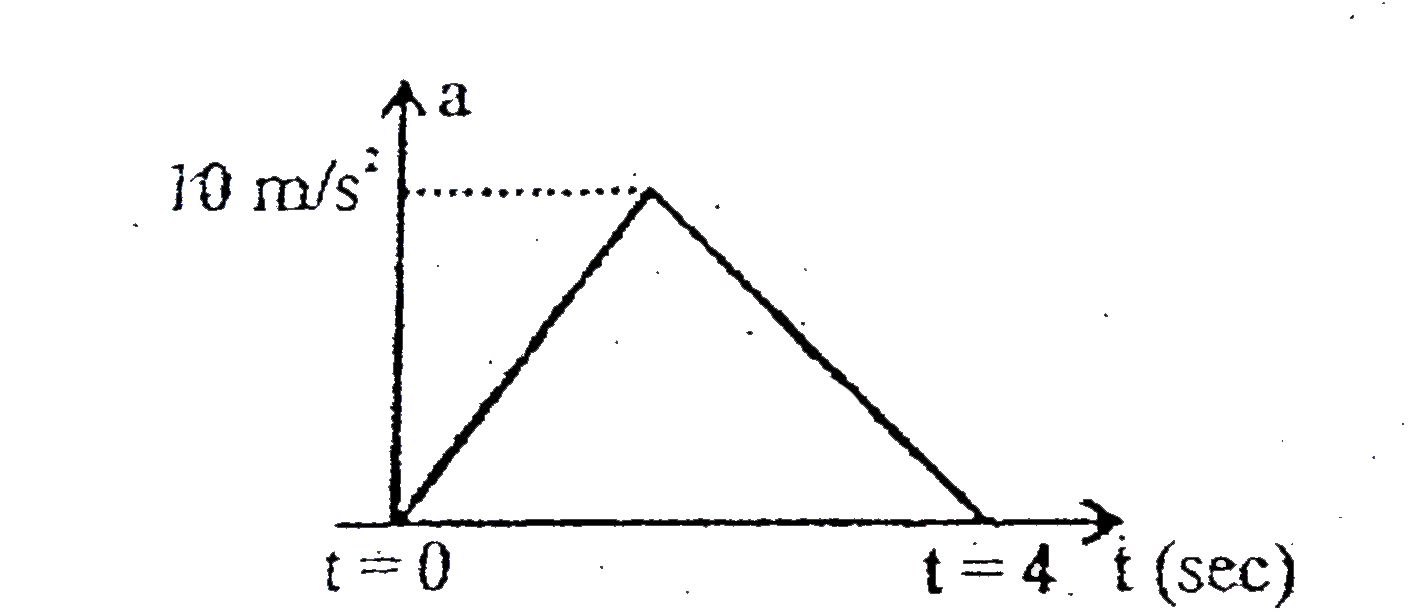 View Solution
View Solution
