The electric flux for Gaussian surface A that enclose the charge particles in free space is (given q1=−14nC,q2=78.85nC,q3=−56nC)

103Nm2/C
103C/Nm2
632×103Nm2/C
632×103C/Nm2
The correct Answer is:A
Net charge enclosed by the surface A
=[−14+78.85−56]×10−9 (∵1nC=10−9C)
=8.85×10−9C
Gaussian surface B does not have a charge.
By gauss's law,
ϕ=qnetε0=8.85×10−98.85×10−12=103Nm2/C
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP20videos
ELECTROSTATICS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
- BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -220videos
GRAVITATION
Similar Questions
Electric flux through a closed surface in free space enclosing a charge q is
View SolutionIn the given figure, there are four point charges placed at the vertices of a square of side, a=1.4m. If q1=+18nC,q2=−24nC,q3+35nCandq4=+16nCm then find the electric at the centre P of the square Assume the potential to be zero at infinity.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The electric flux through a closed surface area S enclosing charge Q is ϕ If the surface area is doubled, then the flux is
A2ϕBϕ/2Cϕ/4Dϕ - Question 2 - Select One
The electric flux through a chlosed surface area S enclosing charge Q is ϕ. If the surface area is doubled, then the flux is
A2ϕBϕ/2Cϕ/4Dϕ - Question 3 - Select One or More
Consider a Gaussian spherical surface covering a dipole of charge q and -q, then
 Aq∈=0 (net charge enclosed by the spherical surface)Bϕ≠t=0 (net flux coming out the spherical surface)CE=0 at all points on the spherical surface.D∫→E⋅d→s = 0 (surface integral of over the spherical surface)
Aq∈=0 (net charge enclosed by the spherical surface)Bϕ≠t=0 (net flux coming out the spherical surface)CE=0 at all points on the spherical surface.D∫→E⋅d→s = 0 (surface integral of over the spherical surface)
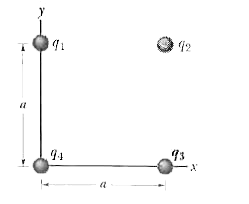
In Fig., the four particles form a square of edge length a = 5.00 cm and have charges q1=+3nC,q2=−15nC,q3=+15nC, and q4=−30nC. In unit-vector notation, what net electric field do the particles produce at the square's center ?
 View Solution
View SolutionWhat is the electric potential at point P, located at the center of the square of charged particles shown in Fig. 24-16a? The distanced is 1.3 m, and the charges are
q1=+12nC, q3=+31nC,
q2=−24nC, q4=+17nC.View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
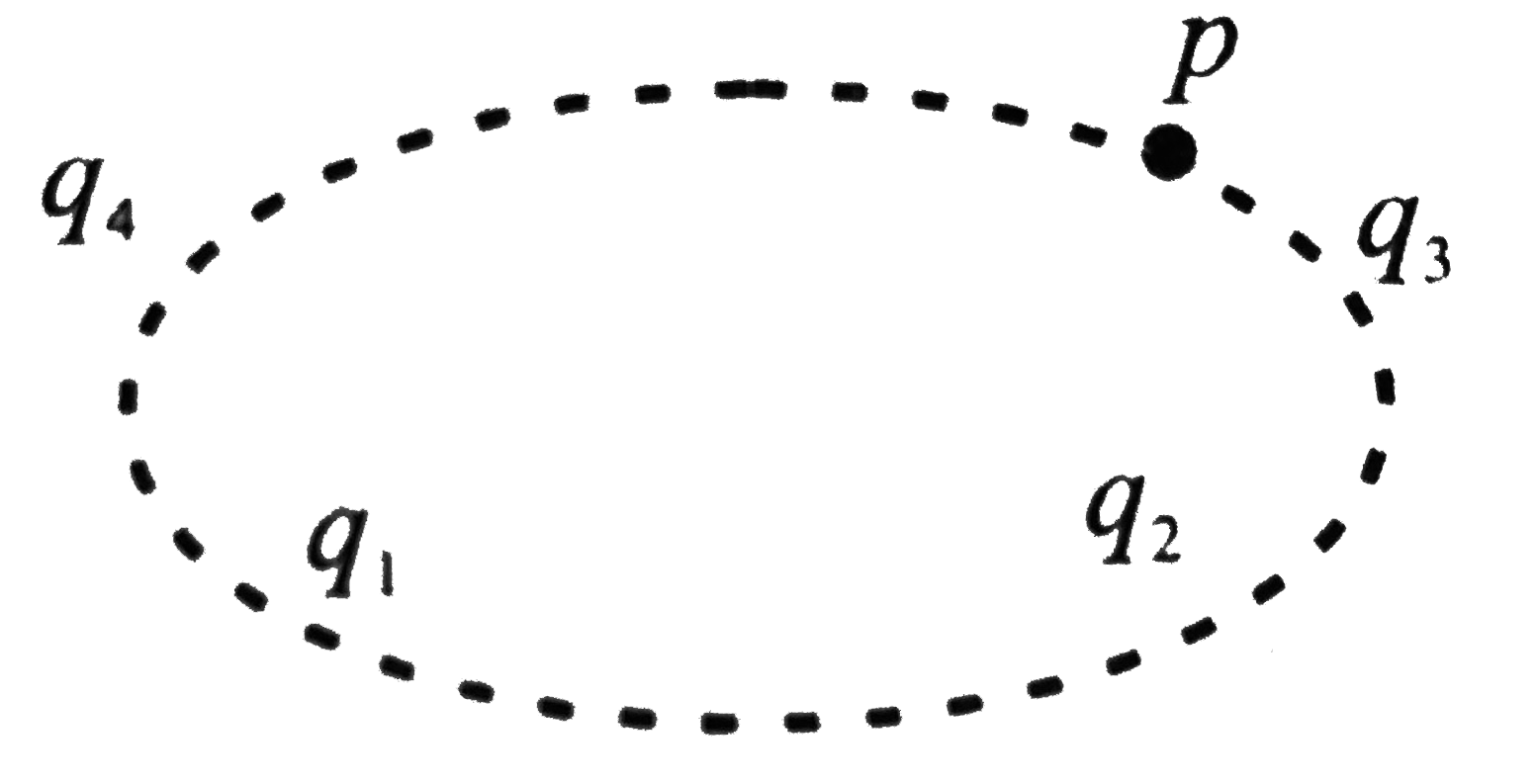
A Gaussian surface encloses two of the four positively charged particles. The particles that contribute to the electric field at a point P on the surface are
 View Solution
View SolutionGauss's law and Coulomb's law , although expressed in different forms , are equivalent ways of describing the relation between charge and electric field in static conditions . Gauss's law is ε0ϕ=qencl,when q(encl) is the net charge inside an imaginary closed surface called Gaussian surface. The two equations hold only when the net charge is in vaccum or air .
If the charge q3 and q4 are displaced (always remaining outside the Gaussian surface), then consider the following two statements :
A: Electric field at each point on the Gaussian surface will remain same .
B: The value of ∮→E.d→A for the Gaussian surface will remain same.View SolutionA charge q is enclosed as shown below the electric flux is
 View Solution
View Solution

