The electrostatic field due to a point charge depends on the distance r as $(l / r^{2})$ . Similarly, indicates how each of the following quantities depends on r : (a) Intensity of light from a point source (b) Electrostatic potential due to a point source (c) Electrostatic potential due to a distance r from the center of a charged metallic sphere of radius R $(r < R)$ .

Video Solution

Text Solution

Verified by Experts

(a) For a point source, light intensity obeys inverse
square law, i..e, $1 \propto \frac{1}{r^{2}}$ .
(b) In case of a point charge,
$V = \frac{q}{4 π \in_{0} r} ∴ V \propto r^{- 1}$
(c ) In case of a charged conducting sphere for an internal point $(r < R)$ .
$V_{\in} = V_{s u r f a c e} = \frac{q}{4 π \in R}$ = constant.
$∴ V \propto r^{0},$ i.e, V does not depend on r.

Updated on:21/07/2023

The electrostatic field due to a point charge depends on the distance r as $\frac{1}{r^{2}}$ . Indicate which of the following quantities shows same dependence on r.
AIntensity of light from a point source
BElectrostatic potential due to a point charge.
CElectrostatic potential at a distance r from the centre of a charged metallic spher. Given rlt radius of the sphere.
DNone of these
Electrostatic potentail V at point, distant r from a charge q varies as
A $q / r^{2}$
B $q^{2} / r$
C $q / r$
D $q^{2} / r^{2}$
The variation of electrostatic potential with radial distance r from centre of positively charged metallic thin shell of radius R is given by graph
A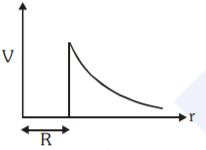
B $# # N \exists T_{R} E_{20}_P H Y_{33}_O 02 # #$
C $# # N \exists T_{R} E_{20}_P H Y_{33}_O 03 # #$
D $# # N \exists T_{R} E_{20}_P H Y_{33}_O 04 # #$