The image of an object placed on the principal axis of a concave mirror of focal length 12 cm is formed at a point which is 10cm more distance form the mirror than the object. The magnification of the image is
8/3
2.5
2
−1.5
The correct Answer is:d.
To solve the problem step by step, we will use the mirror formula and the magnification formula for a concave mirror.
Step 1: Understand the given information
- Focal length of the concave mirror (f) = -12 cm (negative because it's a concave mirror)
- The image is formed at a point which is 10 cm more distance from the mirror than the object.
Step 2: Set up the variables
Let the distance of the object from the mirror be u (which will be negative in the mirror convention). Therefore, the distance of the image from the mirror will be:
v=u+10
Step 3: Apply the mirror formula
The mirror formula is given by:
1f=1u+1v
Substituting the values we have:
1−12=1u+1(u+10)
Step 4: Simplify the equation
Rearranging the equation gives us:
1u+1(u+10)=−112
Finding a common denominator:
(u+10)+uu(u+10)=−112
This simplifies to:
2u+10u(u+10)=−112
Step 5: Cross-multiply to eliminate the fraction
Cross-multiplying gives:
12(2u+10)=−u(u+10)
Expanding both sides:
24u+120=−u2−10u
Step 6: Rearrange the equation
Rearranging gives:
u2+34u+120=0
Step 7: Solve the quadratic equation
Using the quadratic formula u=−b±√b2−4ac2a:
Here, a=1,b=34,c=120:
u=−34±√342−4⋅1⋅1202⋅1
Calculating the discriminant:
342−480=1156−480=676
Thus:
u=−34±262
Calculating the two possible values:
1. u=−82=−4 (not valid since distance cannot be negative)
2. u=−602=−30 (valid)
Step 8: Find the image distance v
Now substituting u=−30 into the equation for v:
v=u+10=−30+10=−20 cm
Step 9: Calculate the magnification
The magnification m is given by:
m=−vu
Substituting the values:
m=−−20−30=2030=23
Final Answer
The magnification of the image is 23.
---
- Focal length of the concave mirror (f) = -12 cm (negative because it's a concave mirror)
- The image is formed at a point which is 10 cm more distance from the mirror than the object.
Let the distance of the object from the mirror be u (which will be negative in the mirror convention). Therefore, the distance of the image from the mirror will be:
v=u+10
The mirror formula is given by:
1f=1u+1v
Substituting the values we have:
1−12=1u+1(u+10)
Rearranging the equation gives us:
1u+1(u+10)=−112
Finding a common denominator:
(u+10)+uu(u+10)=−112
This simplifies to:
2u+10u(u+10)=−112
Cross-multiplying gives:
12(2u+10)=−u(u+10)
Expanding both sides:
24u+120=−u2−10u
Rearranging gives:
u2+34u+120=0
Using the quadratic formula u=−b±√b2−4ac2a:
Here, a=1,b=34,c=120:
u=−34±√342−4⋅1⋅1202⋅1
Calculating the discriminant:
342−480=1156−480=676
Thus:
u=−34±262
Calculating the two possible values:
1. u=−82=−4 (not valid since distance cannot be negative)
2. u=−602=−30 (valid)
Now substituting u=−30 into the equation for v:
v=u+10=−30+10=−20 cm
The magnification m is given by:
m=−vu
Substituting the values:
m=−−20−30=2030=23
The magnification of the image is 23.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
An object is placed on the principle axis of a concave mirror of focal length 10cm at a distance of 21cm from it. A glass slab is placed between the mirror and the object as shown in figure.
Find the distance of final image formed by the mirror.

View SolutionA 1 cm object is placed perpendicular to the principal axis of a convex mirror of focal length 7.5 cm. Find its distance from the mirror if the image formed is 0.6 cm in size.
View Solution
Knowledge Check
An object is placed 40 cm from a concave mirror of focal length 20 cm. The image formed is
AReal, inverted and same in sizeBReal, inverted and smallerCVirtual, erect and largerDVirtual, erect and smallerIf an object is placed 10 cm in front of a concave mirror of focal length 20cm, the image will be
ADiminished, upright, virtualBEnlarged, upright, virtualCDiminished, inverted, realDEnlarged, upright, realAn object is placed at 20 cm from a convex mirror of focal length 10 cm. The image formed by the mirror is
AReal and at 20cm from the mirrorBVirtual and at 20 cm from the mirrorCVirtual and at 20/3cm from the mirrorDReal and at 20/3 cm from the mirror
An object is present on the principal axis of a concave mirror at a distance 30cmfrom it.Focal length of mirror is20cm
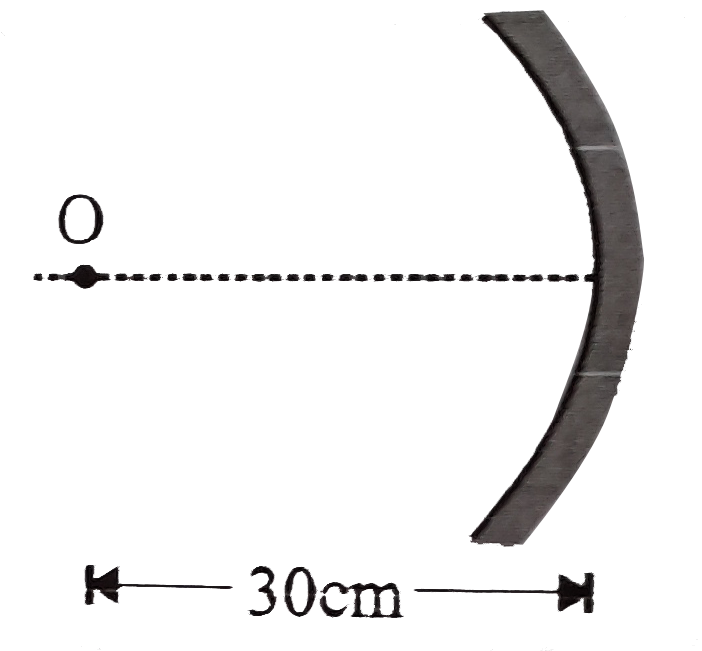
Image formed by mirror is
View SolutionAn object is placed at 15 cm in front of a concave mirror whose focal length is 10 cm. The image formed will be
View SolutionAn object is present on the principal axis of a concave mirror at a distance 30cm from it. Focal length of mirror is 20cm.
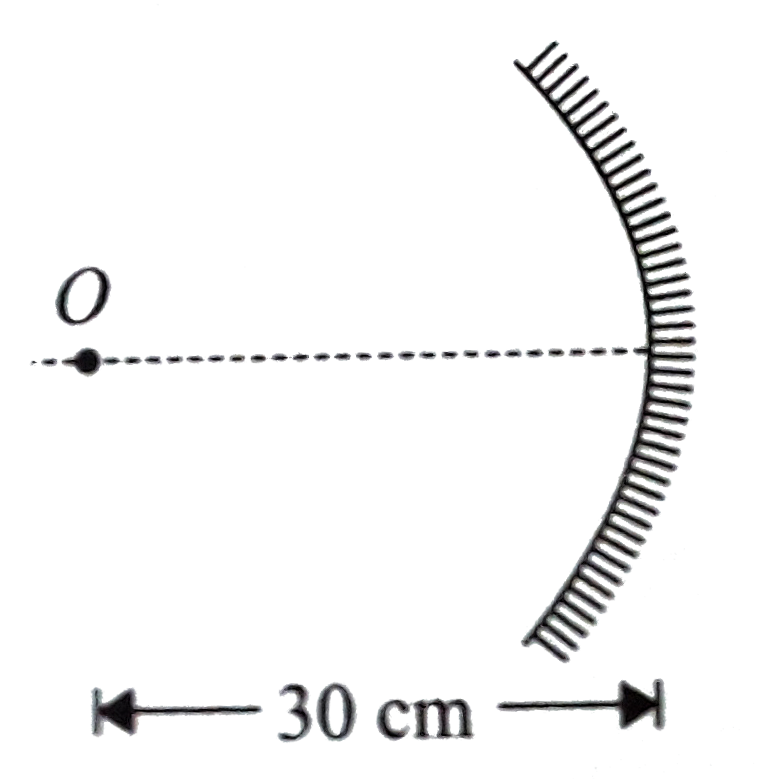
Q. Image formed by mirror is
View SolutionAn object is placed 40 cm from the concave mirror with a focal length of 20 cm. The image formed is:
View SolutionAn object is placed 40 cm from the concave mirror with a focal length of 20 cm . The image formed is :
View Solution
