The law goverening electrostatics is coulomb's law.In priciple coulomb's law can be used to compute electric field due to any charge configuation .In pracitce however it is a formidable task to compute electric field due to uniform charge distributions .For such cases Gauss proposed a theorem which states that
∮¯¯¯E.¯¯¯¯ds=qε0
where ds is an element of area directed across the outward normal for the surface at every point .The integral is called electric flux.Any convenient surface that we choose to evalute the surface integral is called the Gaussian surface.
The SI unit of electric flux is
weber
newton coulomb−1
Volt × metre
joule coulomb−1
The correct Answer is:C
To find the SI unit of electric flux, we start from Gauss's law, which states:
∮E⋅ds=qϵ0
where:
- E is the electric field,
- ds is an area element directed outward,
- q is the charge enclosed,
- ϵ0 is the permittivity of free space.
Step 1: Identify the units of electric field (E)
The electric field E is defined as the force (F) per unit charge (q). The unit of force in SI is Newton (N), and the unit of charge is Coulomb (C). Therefore, the unit of electric field is:
(E)=NC
Step 2: Identify the units of area (ds)
The area element ds is measured in square meters (m²). Thus, the unit of area is:
(ds)=m2
Step 3: Combine the units to find the unit of electric flux
Electric flux (ΦE) is given by the surface integral of the electric field over an area:
ΦE=∮E⋅ds
The unit of electric flux can be derived from the product of the units of electric field and area:
(ΦE)=(E)⋅(ds)=(NC)⋅(m2)
Substituting the units, we get:
(ΦE)=N⋅m2C
Step 4: Convert Newton to Joules
Recall that 1 Newton (N) is equal to 1 Joule per meter (J/m). Therefore, we can express the unit of electric flux as:
(ΦE)=(J/m)⋅m2C=J⋅mC
Step 5: Final expression for the unit of electric flux
Thus, the SI unit of electric flux can be expressed as:
(ΦE)=J⋅mC
Conclusion
The SI unit of electric flux is Joule-meter per Coulomb (J·m/C), which can also be expressed in terms of volts:
(ΦE)=V⋅m
- E is the electric field,
- ds is an area element directed outward,
- q is the charge enclosed,
- ϵ0 is the permittivity of free space.
The electric field E is defined as the force (F) per unit charge (q). The unit of force in SI is Newton (N), and the unit of charge is Coulomb (C). Therefore, the unit of electric field is:
The area element ds is measured in square meters (m²). Thus, the unit of area is:
Electric flux (ΦE) is given by the surface integral of the electric field over an area:
Recall that 1 Newton (N) is equal to 1 Joule per meter (J/m). Therefore, we can express the unit of electric flux as:
Thus, the SI unit of electric flux can be expressed as:
The SI unit of electric flux is Joule-meter per Coulomb (J·m/C), which can also be expressed in terms of volts:
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Taking it together
105 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Knowledge Check
Assertion : The electric field due to a discrete charge configuration is not defined at the locations of the discrete charges.
Reason : For a surface charge distribution, electric field is discontinuous across the surface.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
Coulomb's law is analogous to
View SolutionCalculate electric field due to a charge uniformly distributed in a spherical volume
View SolutionCoulomb's law is valid for
View SolutionFind the direction of electric field at P for the charge distribution as shown infigure.
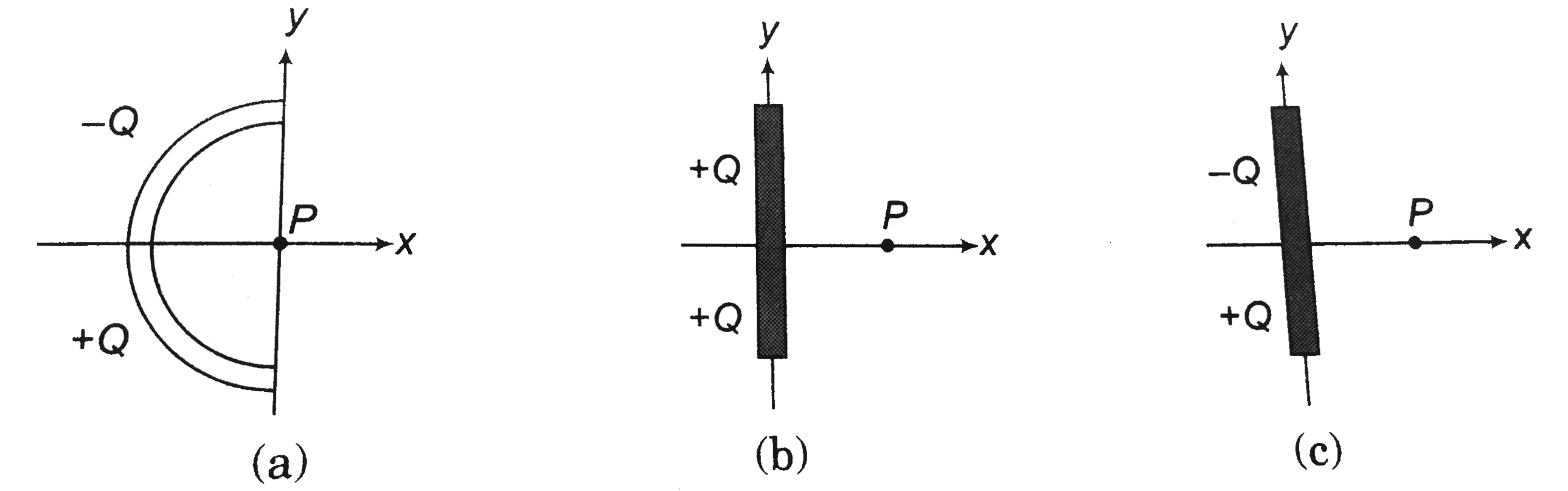
View SolutionWrite Coulomb.s law in vector form.
View SolutionState Gauss's law in electrostatics. Using this law derive an expression for the electric field due to a uniformly charged infinite plane sheet.
View SolutionThe lines of force of the electric field due to two charges q and Q are sketched in the figure. State if
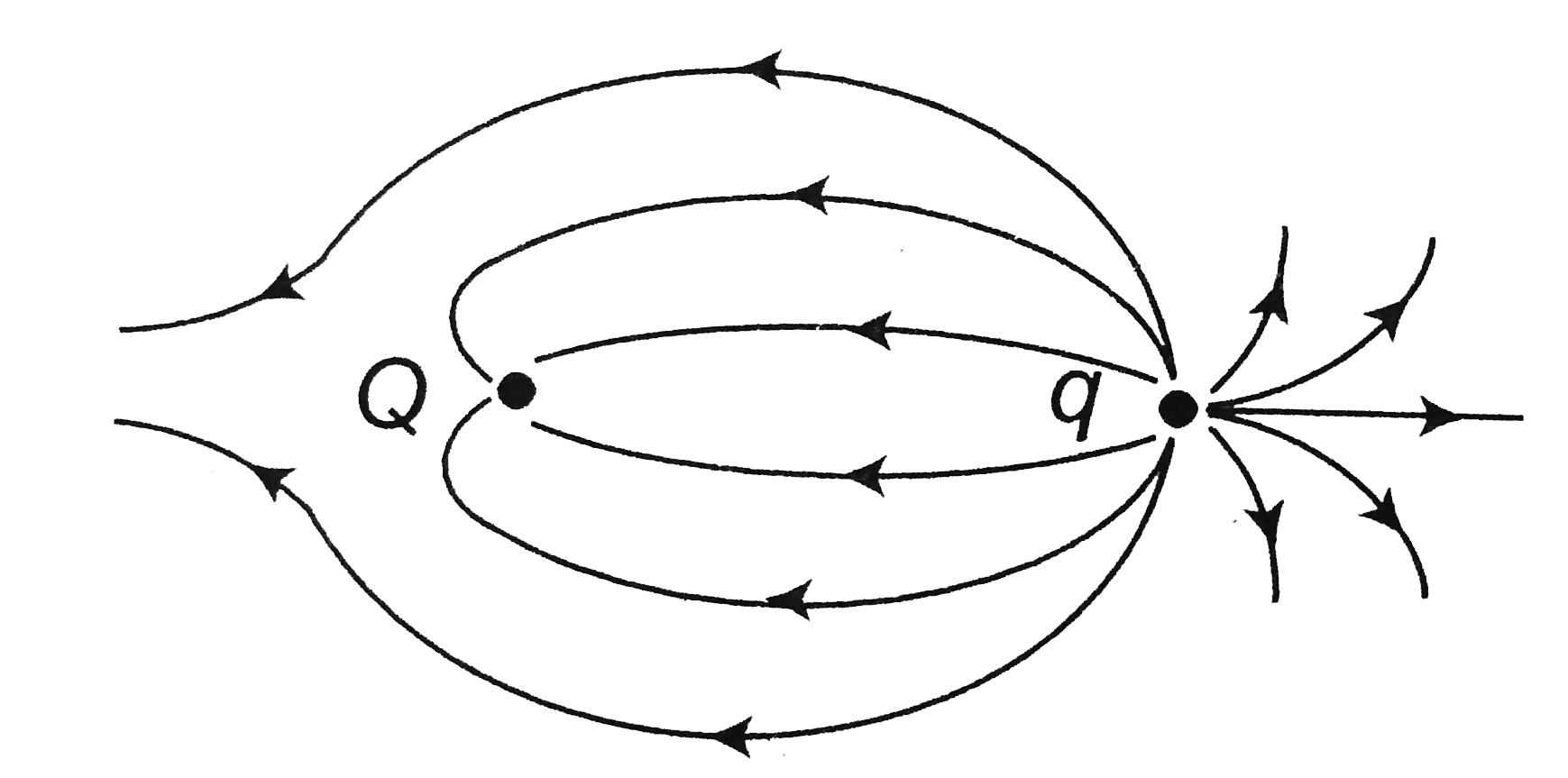
View Solution
