The maximum range of a projectile is 500m. If the particle is thrown up a plane is inclined at an angle of 30∘ with the same speed, the distance covered by it along the inclined plane will be:
250 m
500 m
750m
1000 m
The correct Answer is:B
To solve the problem, we need to find the distance covered by a projectile along an inclined plane when it is thrown with the same speed that gives it a maximum range of 500 m. The incline is at an angle of 30 degrees.
1. Understand the Maximum Range:
The maximum range R of a projectile is given by the formula:
R=u2sin(2θ)g
where u is the initial velocity, g is the acceleration due to gravity, and θ is the angle of projection. For maximum range, θ=45∘.
2. Substituting Values:
Given that the maximum range R=500 m, we can substitute this into the equation:
500=u2sin(90∘)g
Since sin(90∘)=1, this simplifies to:
500=u2g
3. Rearranging for u2:
Rearranging the equation gives:
u2=500g
4. Finding Distance Along the Inclined Plane:
When the projectile is thrown up an inclined plane at an angle of 30∘, we can use the kinematic equation:
v2−u2=2as
Here, v=0 (the final velocity at the highest point), u2=500g, and a=−gsin(30∘).
5. Substituting Values:
Since sin(30∘)=12, we have:
a=−g⋅12=−g2
Plugging in the values into the kinematic equation:
0−(500g)=2(−g2)s
Simplifying this gives:
−500g=−gs
6. Solving for s:
Dividing both sides by −g (assuming g≠0):
s=500 m
Final Answer:
The distance covered by the projectile along the inclined plane is 500 m.
The maximum range R of a projectile is given by the formula:
R=u2sin(2θ)g
where u is the initial velocity, g is the acceleration due to gravity, and θ is the angle of projection. For maximum range, θ=45∘.
Given that the maximum range R=500 m, we can substitute this into the equation:
500=u2sin(90∘)g
Since sin(90∘)=1, this simplifies to:
500=u2g
Rearranging the equation gives:
u2=500g
When the projectile is thrown up an inclined plane at an angle of 30∘, we can use the kinematic equation:
v2−u2=2as
Here, v=0 (the final velocity at the highest point), u2=500g, and a=−gsin(30∘).
Since sin(30∘)=12, we have:
a=−g⋅12=−g2
Plugging in the values into the kinematic equation:
0−(500g)=2(−g2)s
Simplifying this gives:
−500g=−gs
Dividing both sides by −g (assuming g≠0):
s=500 m
The distance covered by the projectile along the inclined plane is 500 m.
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Multiple Correct Answer Type
26 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is
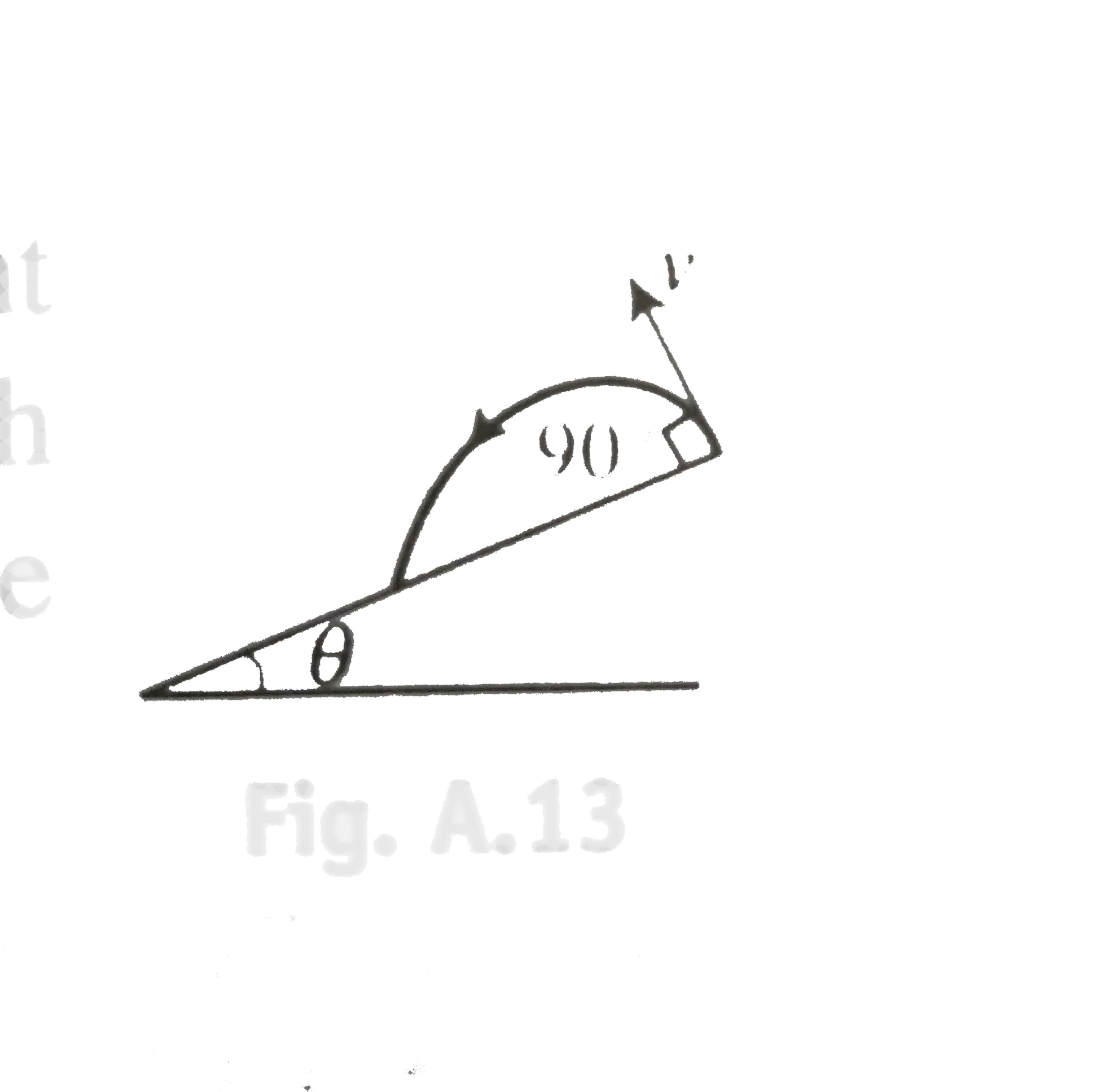
View SolutionA thin uniform circular ring is rolling down an inclined plane of inclination 30∘ without slipping. Its linear acceleration along the inclined plane will be
View SolutionA thin uniform circular ring is rolling down an inclined plane of inclination 30∘ without slipping. Its linear acceleration along the inclined plane will be
View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View SolutionA particle is projected on an inclined plane with a speed u as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
 .
.
View SolutionA thin uniform circular ring is rolling down an inclined plane of inclination 30∘ without slipping. Its linear acceleration along the inclined plane is :
View SolutionAn object is thrown along a direction inclined at an angle of 45∘ with the horizontal direction. The horizontal range of the particle is equal to
View SolutionA body of mass m1 projected vertically upwards with an initial velocity 'u' reaches a maximum height 'h'. Another body of mass m2 is projected along an inclined plane making an angle 30∘ with the horizontal and with speed 'u'. The maximum distance travelled along the incline is
View Solution
