The plates of a 50(μ)F capacitor charged to 400(μ)C are connected through a resistance of 1.0k(ohm). Find the charge remaining on the capacitor 1s after the connection is made.
To solve the problem step by step, we will use the formula for the charge remaining on a capacitor after a certain time when it is connected through a resistor.
Step 1: Identify the given values
- Initial charge on the capacitor, Q0=400μC=400×10−6C
- Capacitance of the capacitor, C=50μF=50×10−6F
- Resistance, R=1.0kΩ=1000Ω
- Time, t=1s
Step 2: Write the formula for charge remaining on the capacitor
The charge remaining on the capacitor at time t is given by the formula:
Q(t)=Q0⋅e−tRC
Step 3: Calculate the time constant RC
First, we need to calculate the product RC:
RC=R⋅C=1000Ω⋅50×10−6F=0.05s
Step 4: Substitute the values into the formula
Now we can substitute Q0, t, and RC into the formula:
Q(1)=400×10−6⋅e−10.05
Step 5: Calculate the exponent
Calculate the exponent:
−10.05=−20
Step 6: Calculate e−20
Now, we need to find e−20. This is a very small number, approximately:
e−20≈1.39×10−9
Step 7: Calculate the remaining charge
Now substitute e−20 back into the equation:
Q(1)=400×10−6⋅1.39×10−9
Q(1)≈5.56×10−13C
Step 8: Final result
Thus, the charge remaining on the capacitor after 1 second is approximately:
Q(1)≈5.56×10−13C
- Initial charge on the capacitor, Q0=400μC=400×10−6C
- Capacitance of the capacitor, C=50μF=50×10−6F
- Resistance, R=1.0kΩ=1000Ω
- Time, t=1s
The charge remaining on the capacitor at time t is given by the formula:
Q(t)=Q0⋅e−tRC
First, we need to calculate the product RC:
RC=R⋅C=1000Ω⋅50×10−6F=0.05s
Now we can substitute Q0, t, and RC into the formula:
Q(1)=400×10−6⋅e−10.05
Calculate the exponent:
−10.05=−20
Now, we need to find e−20. This is a very small number, approximately:
e−20≈1.39×10−9
Now substitute e−20 back into the equation:
Q(1)=400×10−6⋅1.39×10−9
Q(1)≈5.56×10−13C
Thus, the charge remaining on the capacitor after 1 second is approximately:
Q(1)≈5.56×10−13C
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - worked out Example
33 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Objective 1
15 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
A 20(μ)Fcapacitor is joined to a battery of emf 6.0V through a resistance of 100(Ω).find the charge on the capacitor 2.0ms after the connections are made .
View SolutionThe plates of a capacitor of capacitance 10(μ)F,charged to 60(μ)C,are joined together by a wire of resistance 10(Ω)at t=0.Find the charge on the capacitor in the circuit at (a)t=0,(b)t=30(mu)s,(c )t=120(mu)s and (d)t=1.0ms.
View SolutionA capacitor of capacitance 8.0(μ)F is connected to a bettery of emf 6.0V through a resistance of 24(Ω).Find the current in the circuit (a)just after the connections are made and (b)one time constant after the connections are made.
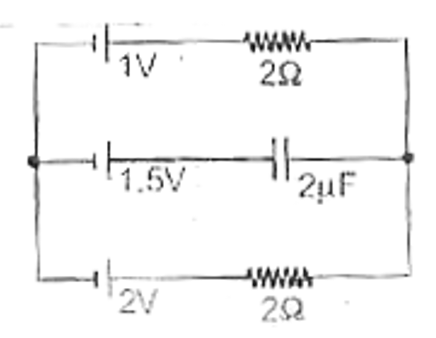
View SolutionThe charge in the 2μF capacitor at steady state is
View SolutionA 5.0(μ)F capacitor having a charge of (20(μ)C)is discharged through a wire aof resistance (5.0Ω). Find the heat dissipated in the wire between 25 to 50 (mu)s after the connections are made.
View SolutionA parallel-plalte capacitor has plate area 20cm2,plate separation 1.0mm and a dielectric slab of dielaectric constant 5.0 filling up the space between the plates.This capacitor is joined to a battery of emf 6.0V through a 100k(Ω)resistor.find the energy of the capacitor 8.9(μ)safter the connections are made.
View SolutionA capacitor of capacitance C is given a charge Q. At t=0,it is connected to an uncharged of equal capacitance through a resistance R. Find the charge on the second capacitor as a function of time.
View SolutionIn steady state, find the charge on the capacitor in (μC) shown in figure.
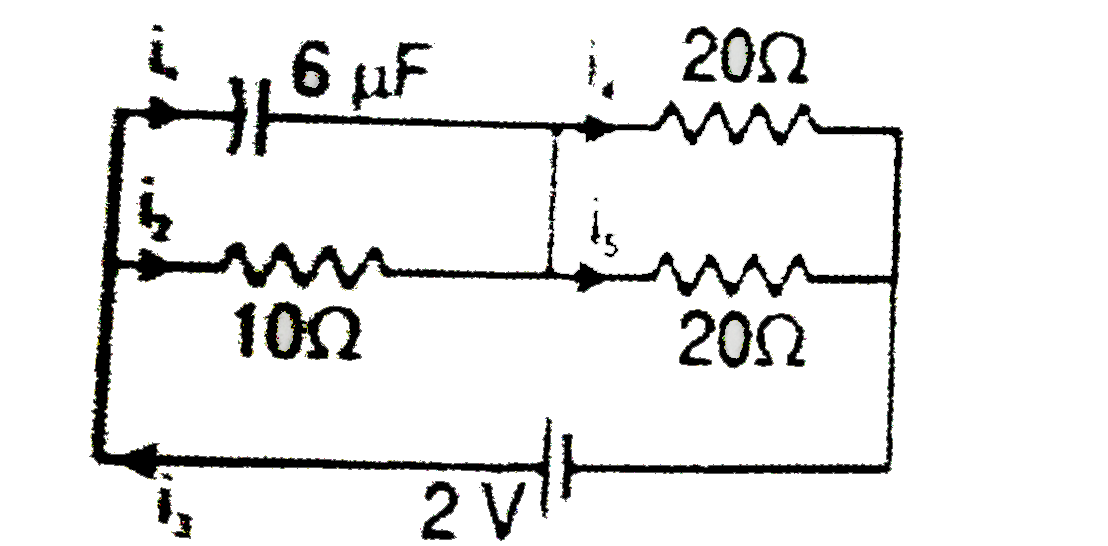
View SolutionA capacitor of capacitance C is given a charge q0. At time t=0 it is connected to an uncharged capacitor of equal capacitance through a resistance R. Find the charge on the first capacitor and the second capacitor as a function of time t. Also plot the corresponding q-t graphs.
View SolutionThree capacitors of capacitances 2μF, 3μF and 6μF are connected in series with a 12 V battery. All the connecting wire are disconnected, the three positive plates are connected together and the three negative plates are connected together. Find the charges on the three capacitors after the reconnection.
View Solution
