The potential energy U of a moving particle of mass m varies with x as shown in figure. The de Broglie wavelengths of the particle in the regions $0 \leq x \leq 1 and x > 1 are λ_{1} and λ_{2}$ respectively. If the total energy of the particle is nE, find $\frac{λ_{1}}{λ_{2}}$

Text Solution

Verified by Experts

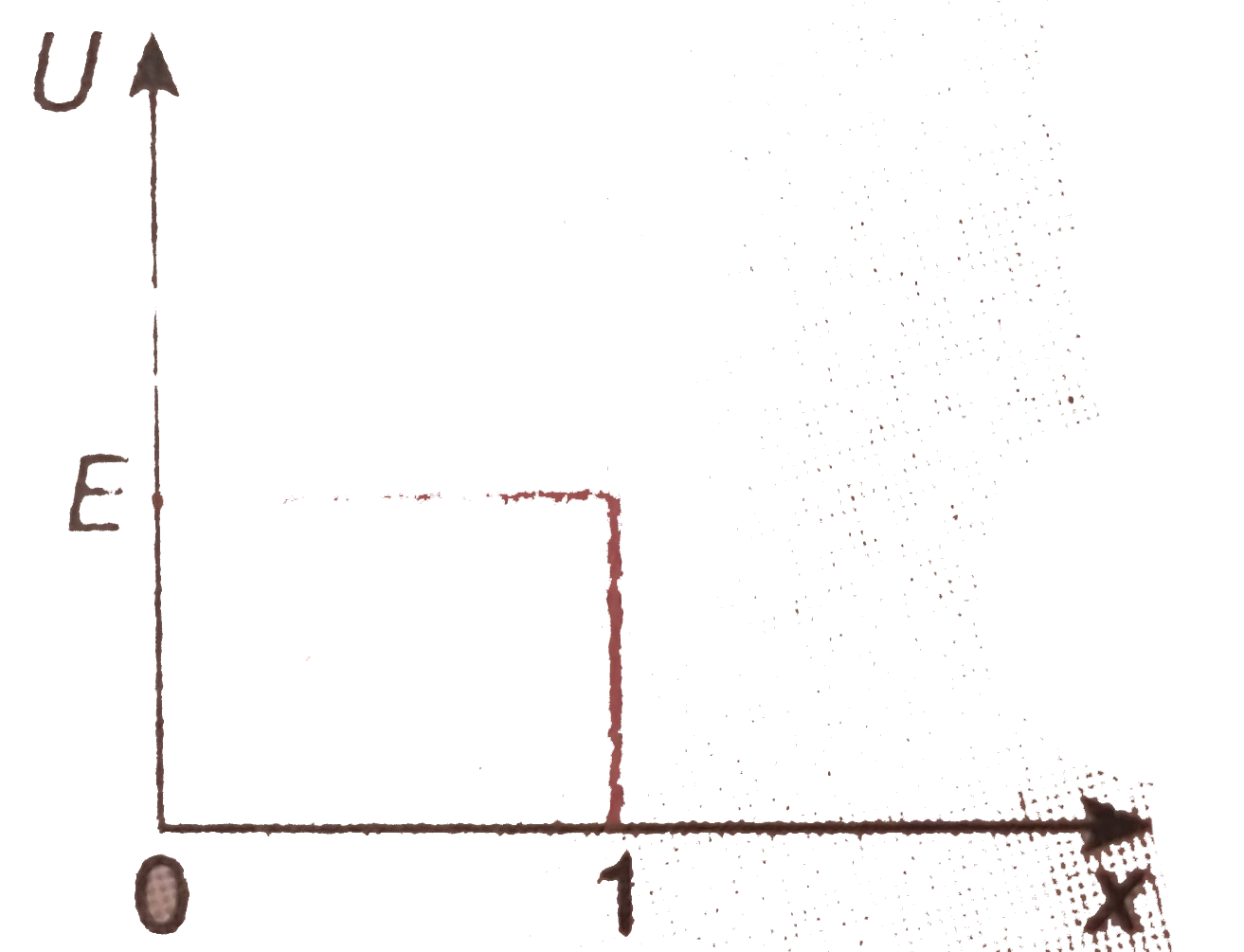
Total energy = nE = potential energy + kinetic energy
In the region $0 \leq x \leq 1$ , potential energy, $U_{1} = E$
$∴$ Kinetic energy is $K_{1} = n E - E = (n - 1) E$
$∴$ de Broglie wavelength,
$λ_{1} = \frac{h}{\sqrt{2 m K_{1}}} = \frac{h}{\sqrt{2 m (n - 1) E}}$ ...(1)
In the region $x > 1$ , potential energy, $U_{2} = 0$
$∴$ Kinetic energy, $K_{2} = n E - 0 = n E$
$∴$ de Broglie wavelength,
$λ_{2} = \frac{h}{\sqrt{2 m K_{2}}} = \frac{h}{\sqrt{2 m n E}}$
From equation (1) and (2) we get,
$\frac{λ_{1}}{λ_{2}} = \frac{h}{\sqrt{2 m (n - 1)}} \times \frac{\sqrt{2 m n E}}{h} = \sqrt{\frac{n}{n - 1}}$

|

Updated on:21/07/2023

Class 12 PHYSICS NUCLEAR PHYSICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The potential energy of particle of mass m varies as
$U (x) = {\begin{matrix} E_{0} for 0 \leq x \leq 1 0 for > 1 \end{matrix}$
The de Broglie wavelength of the particle in the range $0 \leq x \leq 1 is λ_{1}$ and that in the range $x > 1 is λ_{2}$ .
If the total of the particle is $2 E_{0}, find λ_{1} / λ_{2}$ .
A $\sqrt{2}$
B $\sqrt{3}$
C $\sqrt{\frac{1}{2}}$
D $\sqrt{\frac{2}{3}}$
Question 2 - Select One
The potential energy of particle of mass m varies as
$U (x) = {\begin{matrix} E_{0} for 0 \leq x \leq 1 0 for > 1 \end{matrix}$
The de Broglie wavelength of the particle in the range $0 \leq x \leq 1 is λ_{1}$ and that in the range $x > 1 is λ_{2}$ .
If the total of the particle is $2 E_{0}, find λ_{1} / λ_{2}$ .
A $\sqrt{2}$
B $\sqrt{3}$
C $\sqrt{\frac{1}{2}}$
D $\sqrt{\frac{2}{3}}$
Question 3 - Select One
The potential energy of a particle of mass m is given by $U (x) = \begin{matrix} E_{0} & 0 \leq x \leq 1 0 & x > 1 \end{matrix}$ $λ_{1}$ and $λ_{2}$ are the de-Broglie wavelengths of the particle, when $0 \leq x \leq 1$ and x > 1 respectively. If the total energy of particle is $2 E_{0}$ . find ${(λ_{1} / λ_{2})}_{1}^{2}$
A1
B2
C3
D $1 / 2$

CHHAYA PUBLICATION-QUANTUM THEORY-Higher Order Thinking Skill (HOTS) Questions

Home
Ask Doubt
Profile