The potential of a point B (-20m, 30m) taking the potential of a point A (30m, -20m) to be zero in an electric field →E=10xˆi−20ˆjNC−1 is
350 V
−100V
300 V
3500 V
The correct Answer is:D
To find the potential at point B given the potential at point A is zero in the electric field →E=10x^i−20^jN/C, we can use the relationship between electric potential and electric field. The potential difference between two points A and B is given by:
VB−VA=−∫BA→E⋅d→r
Step 1: Identify the coordinates
- Point A: (30m,−20m)
- Point B: (−20m,30m)
Step 2: Define the displacement vector
The displacement vector d→r can be expressed as:
d→r=dx^i+dy^j
Step 3: Calculate the dot product →E⋅d→r
The electric field vector is:
→E=10x^i−20^j
Now, we compute the dot product:
→E⋅d→r=(10x^i−20^j)⋅(dx^i+dy^j)=10xdx−20dy
Step 4: Set up the integral
The potential difference can be expressed as:
VB−VA=−∫BA(10xdx−20dy)
Since VA=0, we have:
VB=−∫BA(10xdx−20dy)
Step 5: Determine the limits of integration
- For x: from xA=30 to xB=−20
- For y: from yA=−20 to yB=30
Step 6: Evaluate the integral
We can separate the integral:
VB=−(∫−203010xdx+∫30−20(−20)dy)
Calculating the first integral:
∫10xdx=5x2
Evaluating from 30 to -20:
5(−202−302)=5(−400−900)=5(−1300)=−6500
Calculating the second integral:
∫−20dy=−20y
Evaluating from -20 to 30:
−20(30−(−20))=−20(50)=−1000
Step 7: Combine the results
Now, substituting back into the equation for VB:
VB=−(−6500−1000)=7500V
Final Answer
The potential at point B is:
VB=7500V
- Point A: (30m,−20m)
- Point B: (−20m,30m)
The displacement vector d→r can be expressed as:
d→r=dx^i+dy^j
The electric field vector is:
→E=10x^i−20^j
Now, we compute the dot product:
→E⋅d→r=(10x^i−20^j)⋅(dx^i+dy^j)=10xdx−20dy
The potential difference can be expressed as:
VB−VA=−∫BA(10xdx−20dy)
Since VA=0, we have:
VB=−∫BA(10xdx−20dy)
- For x: from xA=30 to xB=−20
- For y: from yA=−20 to yB=30
We can separate the integral:
VB=−(∫−203010xdx+∫30−20(−20)dy)
∫10xdx=5x2
Evaluating from 30 to -20:
5(−202−302)=5(−400−900)=5(−1300)=−6500
∫−20dy=−20y
Evaluating from -20 to 30:
−20(30−(−20))=−20(50)=−1000
Now, substituting back into the equation for VB:
VB=−(−6500−1000)=7500V
The potential at point B is:
VB=7500V
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type
94 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
Similar Questions
Find the potential difference VAB between A(2m,1m,0) and B(0,2m,4m) in an electric field,
E=(xˆi−2yˆj+zˆk)Vm
View SolutionA small sphere is charged uniformly and placed at some point A(x0,y0) so that at point B(9m,4m) electric field strength is →E=(54ˆi+72ˆj)NC−1 and potential is 1800V. Then
View SolutionAn electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View SolutionDetermine the potential at a point 0.50 m (i) from a+20μC potential charge (ii) from a−20μC point charge.
View SolutionPotential difference between two points (VA−VB) in an electric field E=(2ˆi−4ˆj)N/C, where A=(0,0) and B=(3m,4m) is
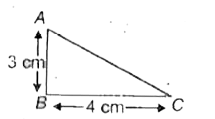
View SolutionABC is a right anlged triangle situated in a uiform electric field →E which is in the plane of the traingle . The points A and B are at the same potential of 15 V while the point C is at a potential of 20 V. AB = 3cm and BC = 4 cm . The magnitude of electric field is (in S.I . Units )
View SolutionFind the potential V at P in the gravitational field of fixed point mass M.
View SolutionAn electric field →E=→IAx exists in the space, where A=10Vm−2. Take the potential at (10m, 20m ) to be zero. Find the potential at the origin.
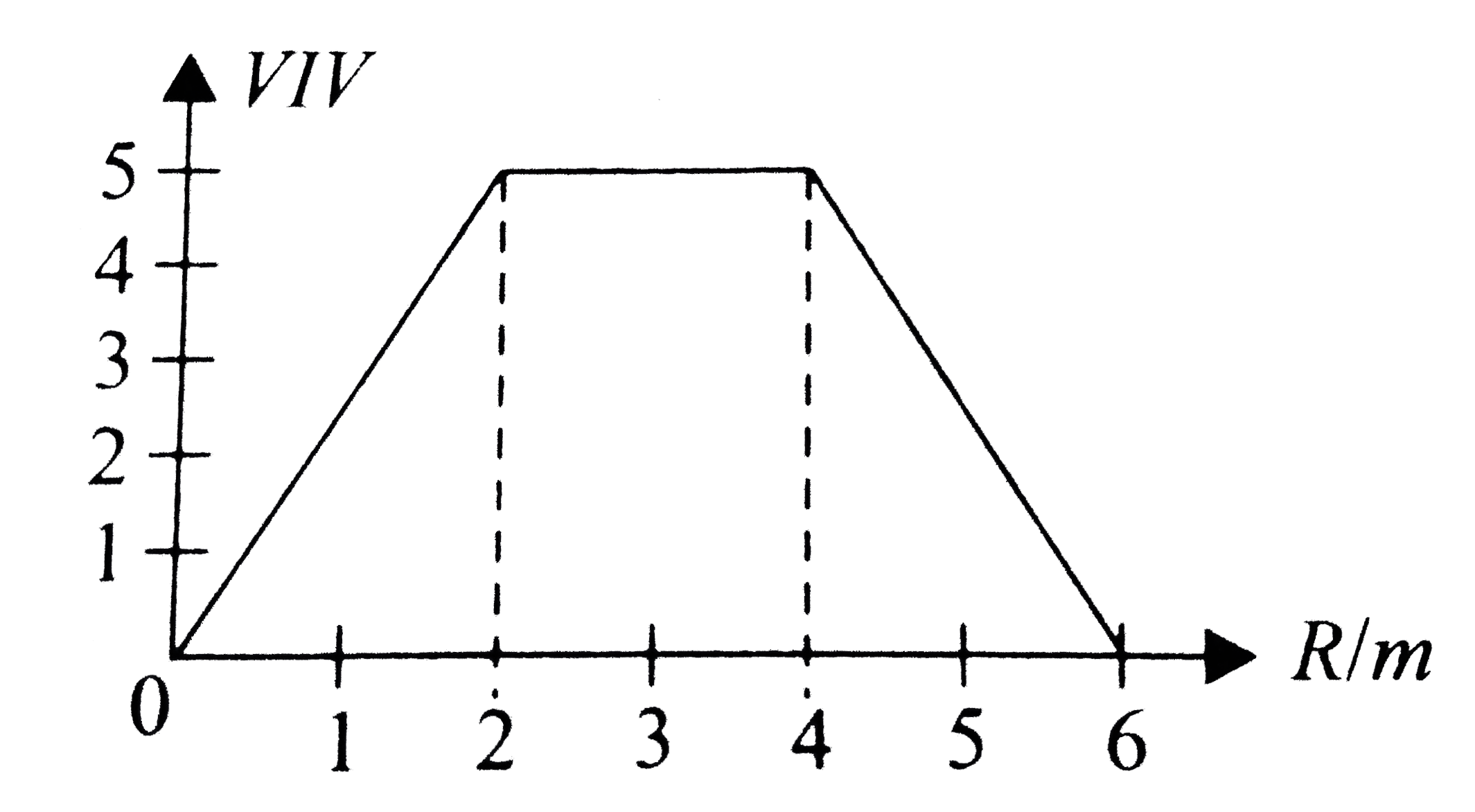
View SolutionThe variation of potential with distance R from the fixed point is shown in (Fig. 3.125).
 .
.
The electric field at R=5m is.
View SolutionThe electric potential V at any point x, y, z (all in meters) in space is given by V=4x2 volts. The electric field at the point (1m, 0, 2m) is……………..V/m.
View Solution
