The temperature at the bottom of a $40 c m$ deep lake is $12^{\circ} C$ and that at the surface is $35^{\circ} C$ . An air bubble of volume $1.0 c m^{3}$ rises from the bottom to the surface. Its volume becomes (atmospheric pressure $= 10 m$ of water)

A

$2.0 c m^{3}$

B

$3.2 c m^{3}$

C

$5.4 c m$

D

$8.0 c m^{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

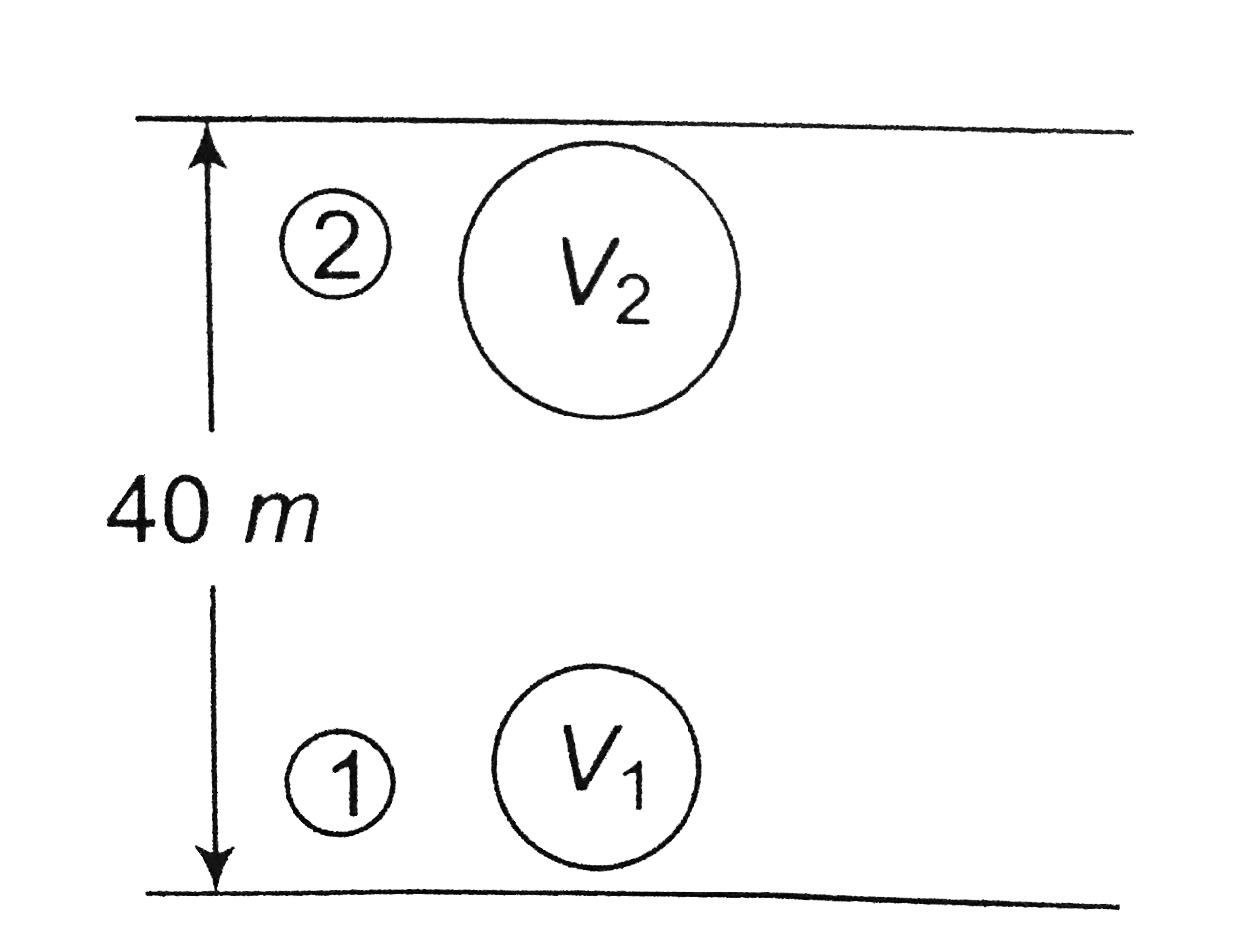
$P_{1} = P_{a t m} + P_{w a t e r} = 10 + 40 = 50 m$ of water
$V_{1} = 1 c c, T_{1} = 12 + 273 = 285 K$
$P_{2} = P_{a t m} = 10 m$ of water
$V_{2} = ?, T_{2} = 35 + 273 = 308 K$
Since number of moles in the bubble remains same
$\frac{P_{1} V_{1}}{R T_{1}} = \frac{P_{2} V_{2}}{R T_{2}}$
$\frac{50 \times 1}{285} = \frac{10 V_{2}}{308} \Rightarrow V_{2} = 5.4 c m^{3}$

|

Updated on:21/07/2023

Class 11 PHYSICS KINETIC THEORY OF GASES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A bubble rises from the bottom of a lake $90 m$ deep on reaching the surface, its volume becomes (take atmospheric pressure equals to $10 m$ of water)
A $4$ times
B $8$ times
C $10$ times
D $3$ times
Question 2 - Select One
At the bottom of a lake where temperature is $7^{0} C$ the pressure is $2.8$ atmosphere. An air bubble of radius $1 c m$ at the bottom rises to the surface. Where the temperature is $27^{0} C$ . Radius of air bubble at the surface is
A $3^{1 / 3}$
B $4^{1 / 3}$
C $5^{1 / 3}$
D $6^{1 / 3}$
Question 3 - Select One
An air bubble starts rising from the bottom of a lake. Its diameter is 3.6 mm at the bottom and 4 mm at the surface. The depth of the lake is 250 cm and the temperature at surface is $40^{\circ} C$ . What is the temperature at the bottom of the lake? Given atmospheric pressure = 76 cm of Hg and $g = 980 c m / s^{2}$
A $11^{\circ} C$
B ${12.36}^{\circ} C$
C $13^{\circ} C$
D ${10.37}^{\circ} C$

CP SINGH-KINETIC THEORY OF GASES-Exercises

Home
Ask Doubt
Profile