The torque τ on a body about a given point is found to be equal to AxxL where A is a constant vector, and L is the angular momentum of the body about that point. From this it follows that
dL/dt is perpendiclar to L at all instants of time
the component of L in the direction of A does not change with time
magnitude of L does not change with time
L does not change with time
The correct Answer is:A, B, C
To solve the problem, we need to analyze the relationship between torque, angular momentum, and the given constant vector A.
1. Understanding Torque and Angular Momentum:
The torque τ on a body about a given point is defined as the rate of change of angular momentum L with respect to time. Mathematically, this is expressed as:
τ=dLdt
2. Given Relationship:
The problem states that the torque is given by:
τ=A×L
where A is a constant vector and L is the angular momentum vector.
3. Perpendicularity of Torque and Angular Momentum:
Since torque τ is given by the cross product A×L, it follows that τ is perpendicular to both A and L. This implies:
τ⊥L
Therefore, the rate of change of angular momentum dLdt is also perpendicular to L at all times.
4. Component of Angular Momentum in Direction of A:
To analyze the component of L in the direction of A, we can express this component as:
L∥A=L⋅^A
where ^A is the unit vector in the direction of A.
5. Differentiating the Component:
We differentiate this component with respect to time:
ddt(L⋅^A)=dLdt⋅^A+L⋅d^Adt
Since A is constant, d^Adt=0. Thus, we have:
ddt(L⋅^A)=dLdt⋅^A=0
This indicates that the component of L in the direction of A does not change with time.
6. Conclusion:
From the above analysis, we can conclude that:
- The torque τ is perpendicular to the angular momentum L at all times.
- The component of angular momentum L in the direction of the constant vector A does not change with time.
Final Answer:
From the given conditions, we conclude that:
1. τ⊥L at all times.
2. The component of L in the direction of A remains constant over time.
The torque τ on a body about a given point is defined as the rate of change of angular momentum L with respect to time. Mathematically, this is expressed as:
τ=dLdt
The problem states that the torque is given by:
τ=A×L
where A is a constant vector and L is the angular momentum vector.
Since torque τ is given by the cross product A×L, it follows that τ is perpendicular to both A and L. This implies:
τ⊥L
Therefore, the rate of change of angular momentum dLdt is also perpendicular to L at all times.
To analyze the component of L in the direction of A, we can express this component as:
L∥A=L⋅^A
where ^A is the unit vector in the direction of A.
We differentiate this component with respect to time:
ddt(L⋅^A)=dLdt⋅^A+L⋅d^Adt
Since A is constant, d^Adt=0. Thus, we have:
ddt(L⋅^A)=dLdt⋅^A=0
This indicates that the component of L in the direction of A does not change with time.
From the above analysis, we can conclude that:
- The torque τ is perpendicular to the angular momentum L at all times.
- The component of angular momentum L in the direction of the constant vector A does not change with time.
From the given conditions, we conclude that:
1. τ⊥L at all times.
2. The component of L in the direction of A remains constant over time.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - AR_TYPE2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - LC_TYPE8videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - SCQ_TYPE29videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
Angular momentum of a planet about the point of it's apogee is
View SolutionThe angular velocity of a rigid body about any point of that body is same :
View SolutionWhen a body is projected at an angle with the horizontal in the uniform gravitational field of the earth, the angular momentum of the body about the point of projection, as it proceeds along its path
View SolutionTwo particle A and B are moving as shown in the figure
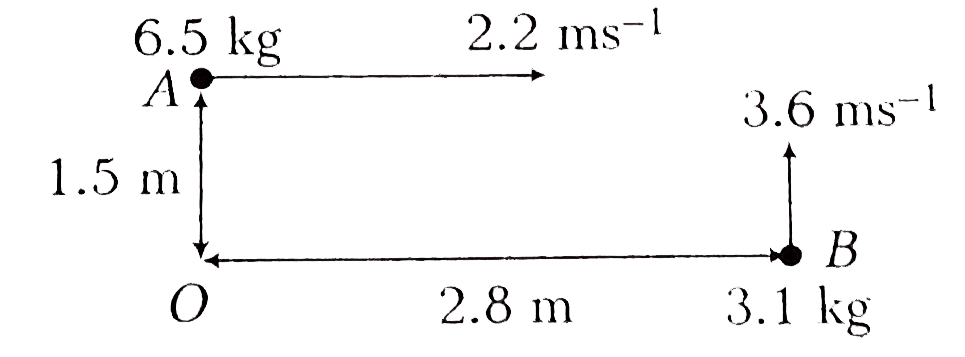
Their total angular momentum about the point O isView SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form :
 View Solution
View SolutionFind the charge on the capacitor shown in figure
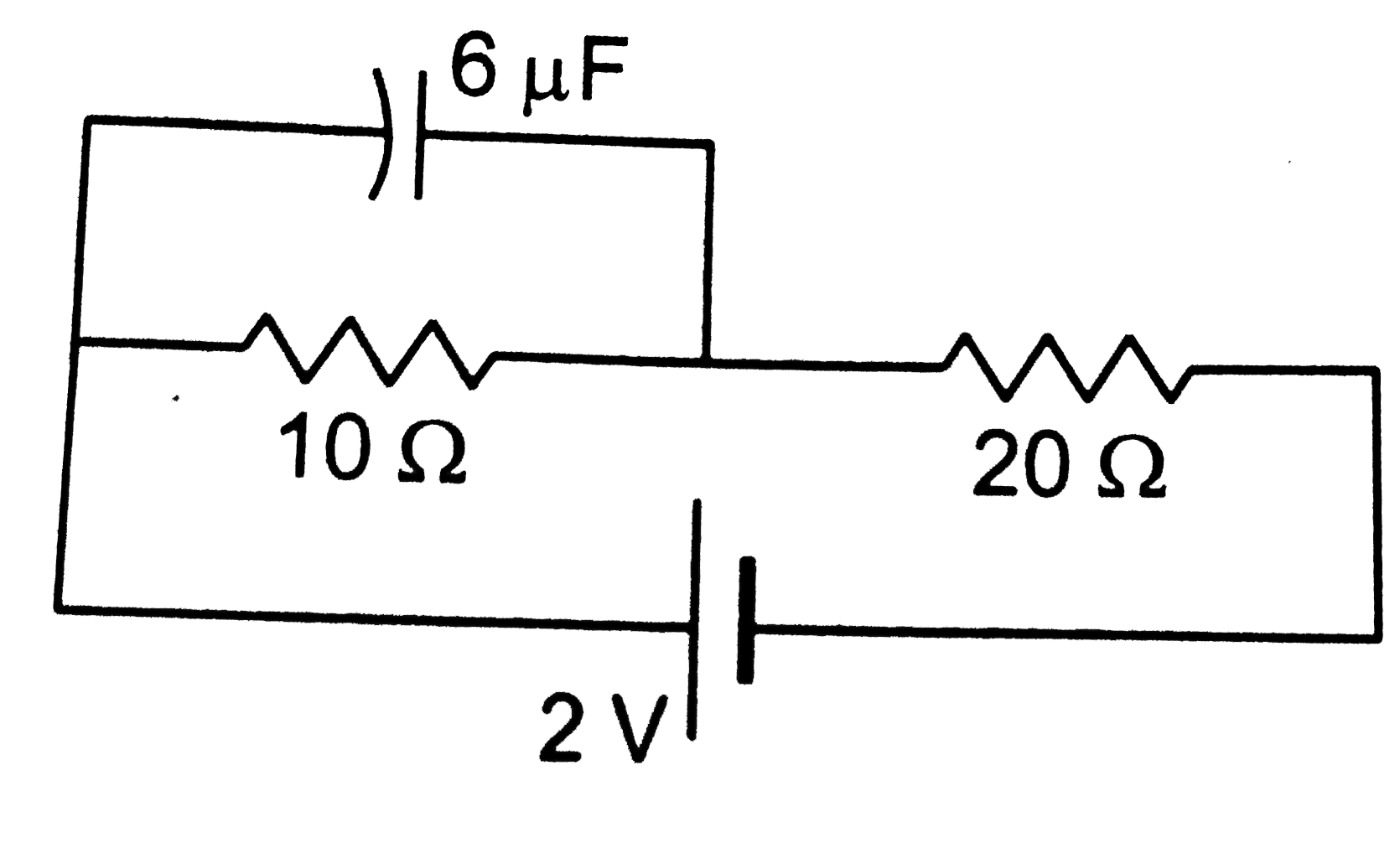 View Solution
View SolutionStatement-1: if there is no external torque on a body about its centre of mass, then the velocity of the center of mass remains constant.
Statement-2: The linear momentum of an isolated system remains constant.View SolutionA particle is moving along a straight line with increasing speed. Its angular momentum about a fixed point on this line :
View SolutionMoment of concurrent forces about any point is constant.
If vector sum of all concurrent forces is zero, then moment of all the forces about any point is also zero.View SolutionA body of mass m is projected with a velocity u at an angle θ with the horizontal. The angular momentum of the body, about the point of projection, when it at highest point on its trajectory is
View Solution
