The velocity of a particle moving in the x direction varies as V=α√x where α is a constant. Assuming that at the moment t=0 the particle was located at the point x=0. Find the acceleration.
v=α√x=αx1/2[Herev=fn(x)]
dvdx=α.12x−1/2
Acceleration a=vdvdx=αx1/2α2x−1/2=α22
Acceleration is constant. Using equation of motion,
v=u+at=0+α22t
=α2t2
Topper's Solved these Questions
Similar Questions
The velocity of a particle moving in the positive direction of the x axis varies as v=α√x, where α is a positive constant. Assuming that at the moment t=0 the particle was located at the point x=0, find:
(a) the time dependence of the velocity and the acceleration of the particle,
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.View SolutionThe velocity of a particle moving in the positive direction of the x axis varies as v=α√x, where α is a positive constant. Assuming that at the moment t=0 the particle was located at the point x=0, find:
(a) the time dependence of the velocity and the acceleration of the particle,
(b) the mean velocity of the particle averaged over the time that the particle takes to cover the first s metres of the path.View Solution
Knowledge Check
- Question 1 - Select One or More
The velocity of a particle moving in the positive direction of x-axis veries as v=10√x. Assuming that at t=0, particle was at x=0
AThe initial velocity of the particle is zeroBthe initial velocity of the particle is 2.5ms.CThe accelration of the particle is 2.5ms2.DThe acceleration of the particle is 50ms2. - Question 2 - Select One
The velocity of a particle moving in the positive direction of X-axis varies as v=5√x. Assuming that at t = 0, particle was at x = 0. What is the acceleration of the particle ?
A12.5ms−2B7.5ms−2C5ms−2D2.5ms−2 - Question 3 - Select One
The velocity v of a particle moving along x - axis varies with ist position (x) as v=α√x, where α is a constant. Which of the following graph represents the variation of its acceleration (a) with time (t)?
A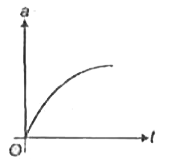 B
B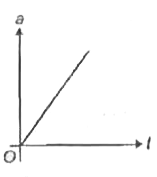 C
C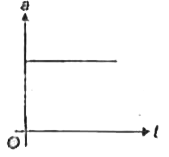 D
D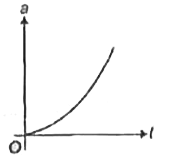
The velocity of a particle moving in the positive direction of the X-axis varies as V=K√S where K is a positive constant. Draw V−t graph.
View SolutionA particle moves in the plane xy with velocity v=ai+bxj, where i and j are the unit vectors of the x and y axes, and a and b are constants. At the initial moment of time the particle was located at the point x=y=0. Find:
(a) the equation of the particle's trajectory y(x),
(b) the curvature radius of trajectory as a function of x.View SolutionThe velocity (v) of a particle of mass m moving along x-axis is given by v=α√x, where α is a constant. Find work done by force acting on particle during its motion from x=0 to x=2m :-
View SolutionThe velocity of a particle moving along the xaxis is given by v=v0+λx, where v0 and lambda are constant. Find the velocity in terms of t.
View SolutionA particle is acted upon by a force given by F=−αx3−βx4 where α and β are positive constants. At the point x = 0, the particle is –
View Solution

