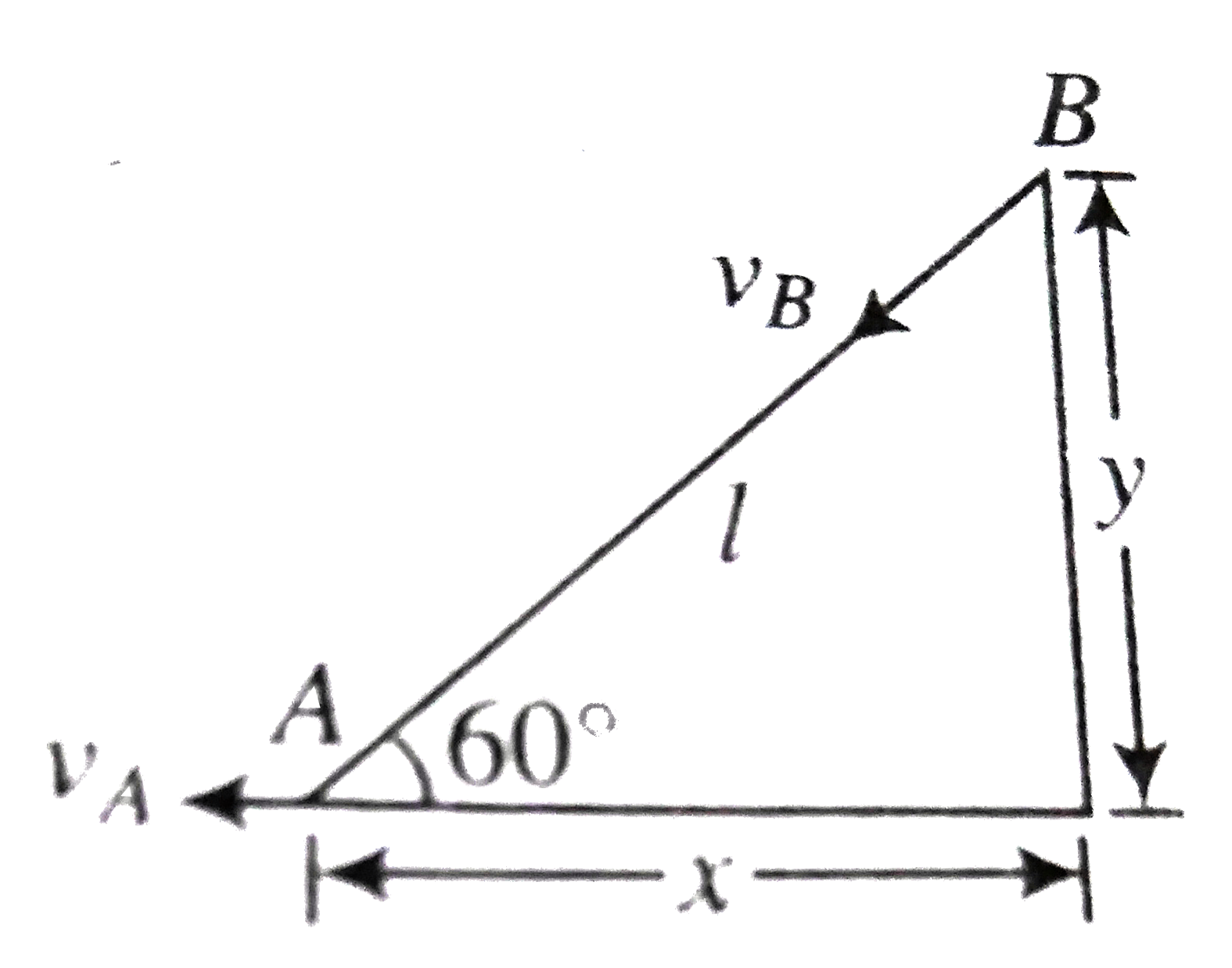
The velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is

2√3ms−1
1ms−1
12√3ms−1
√32ms−1
The correct Answer is:B
Here y is constant dldt=vB
l2=y2+x2
⇒2ldldt=2xdxdt
⇒vB=xlvA=vAcos60∘=1ms−1
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct11videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions

Due to slippoing points A and B on the rim of the disk have the velocities shown. Determine the velocities of the centre point C and point F at this instant.View SolutionThere is a fixed half cylinder of radius R on a horizontal table. A uniform rod of length 2R leans against it as shown. At the instant shown, θ=30∘ and the right end of the rod is sliding with velocity v.
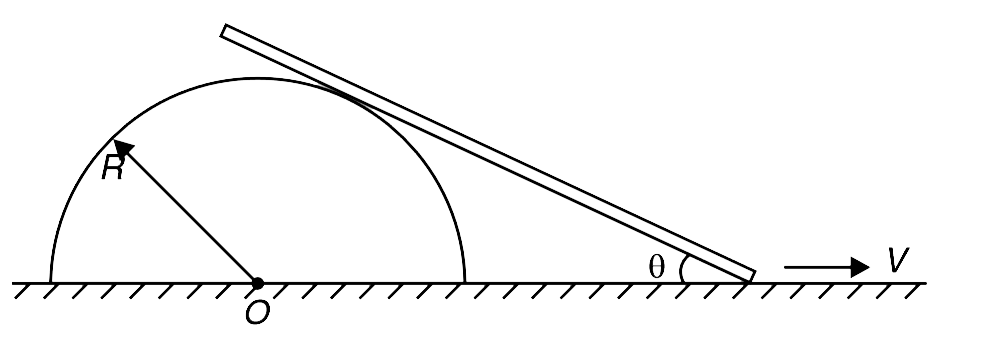
(a) Calculate the angular speed of the rod at this instant.
(b) Find the vertical component of the velocity of the centre of the rod at this instant.View Solution
Knowledge Check
- Question 1 - Select One
A rod of mass m and length l is sliding against a smooth vertical wall as shown. The speed of the bottom end of the rod at the instant shown is V0. The magnitude of angular momentum of the rod about ICR. (instantaneous axis of rotation) at the instant when θ=30∘ is
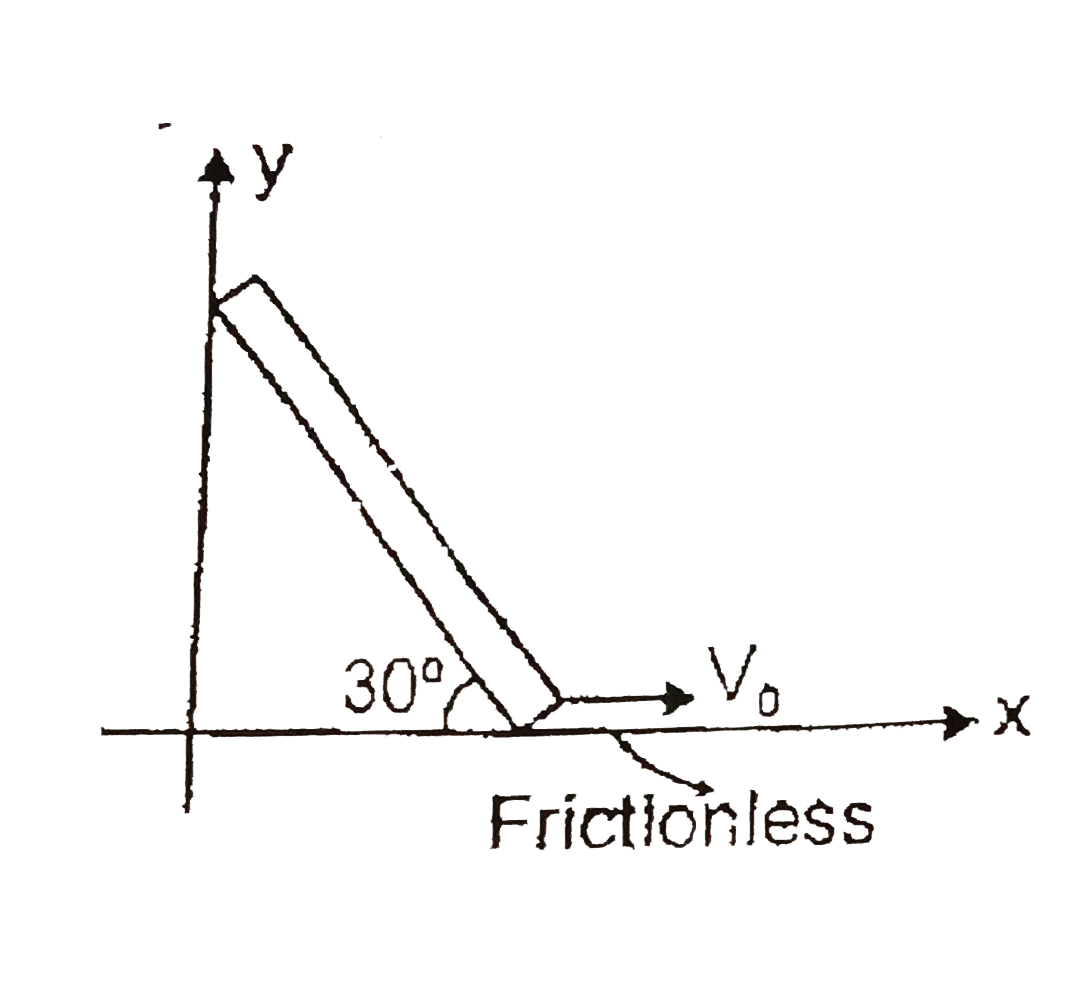 A16mV0lB23mV0lC112mV0lDNone of these
A16mV0lB23mV0lC112mV0lDNone of these - Question 2 - Select One
A rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
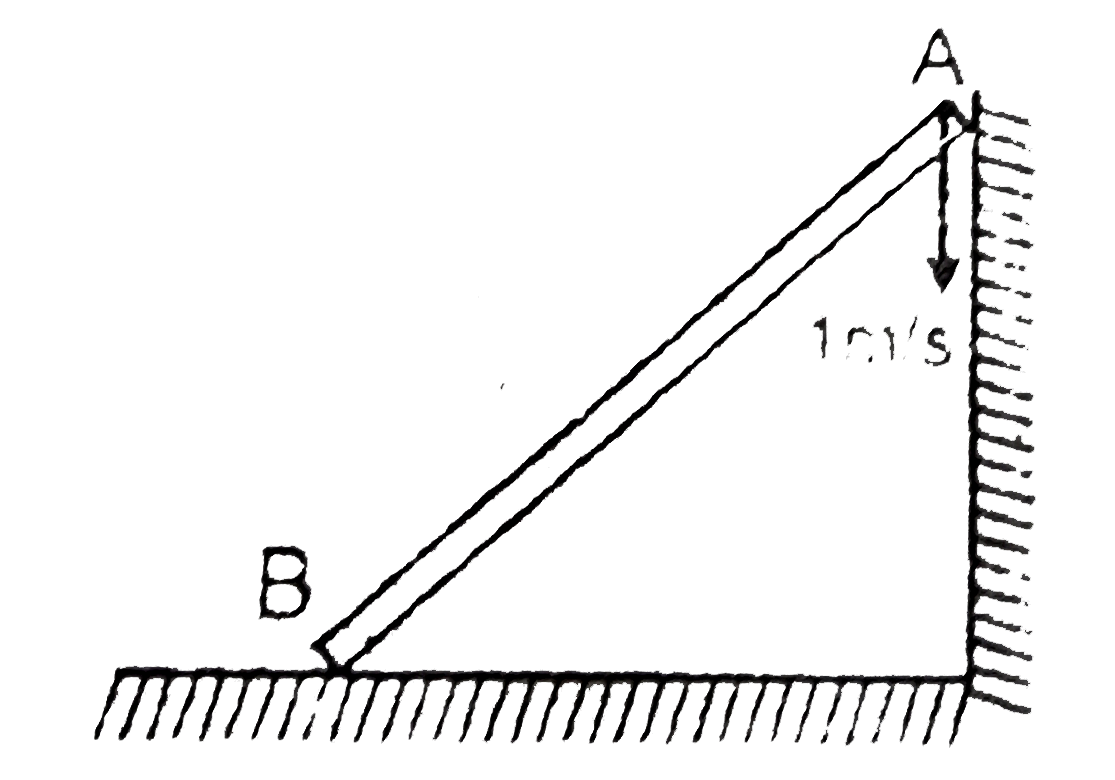 A2 rad/sB1.5 rad/sC0.5 rad/sD0.75 rad/s
A2 rad/sB1.5 rad/sC0.5 rad/sD0.75 rad/s - Question 3 - Select One
A smooth rod OP is fixed vertically. A disc of mass m and radius R is rolling without slipping at the given instant on a rough horizontal surface as shown. Velocity of centre of mass C of disc is v0. A rod AB of length L is connected with disc at A, R/2 distance vertically up from centre of disc with pin joint (about which it can rotate freely), other end of the rod is attached to a small smooth ring B, which can move freely over rod OP. At an instant rod AB makes an angle 60∘ with the vertical. The velocity of ring on the vertical rod at this instant is.
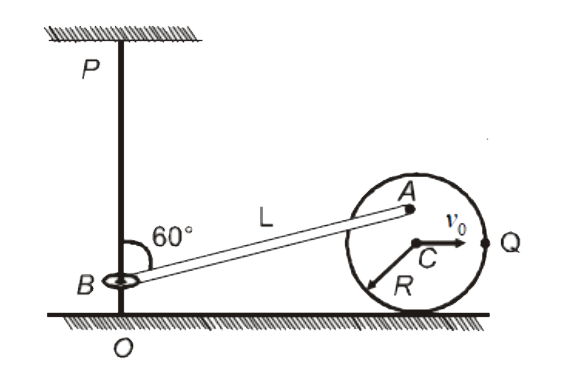 A√32v0B32v0Cv0Dperpendicular to velocity of point Q(Q and C are at same horizontal level)
A√32v0B32v0Cv0Dperpendicular to velocity of point Q(Q and C are at same horizontal level)
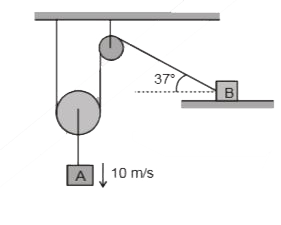
Find velocity of block 'B' at the instant shown in figure :
 View Solution
View SolutionFind velocity of block 'B' at the instant shown in figure.
 View Solution
View SolutionFind the angular velocity of A with respect to O at the instant shown in (Fig. 5.165).
 .View Solution
.View SolutionA uniform rod of length L is rotating about its one end in the horizontal plane under constant aceeleration α starting from rest. Find the linear velocity of its mid-point after time t0. Also, find the normal and tangential components of acceleration of the mid-point of the rod at this instant.
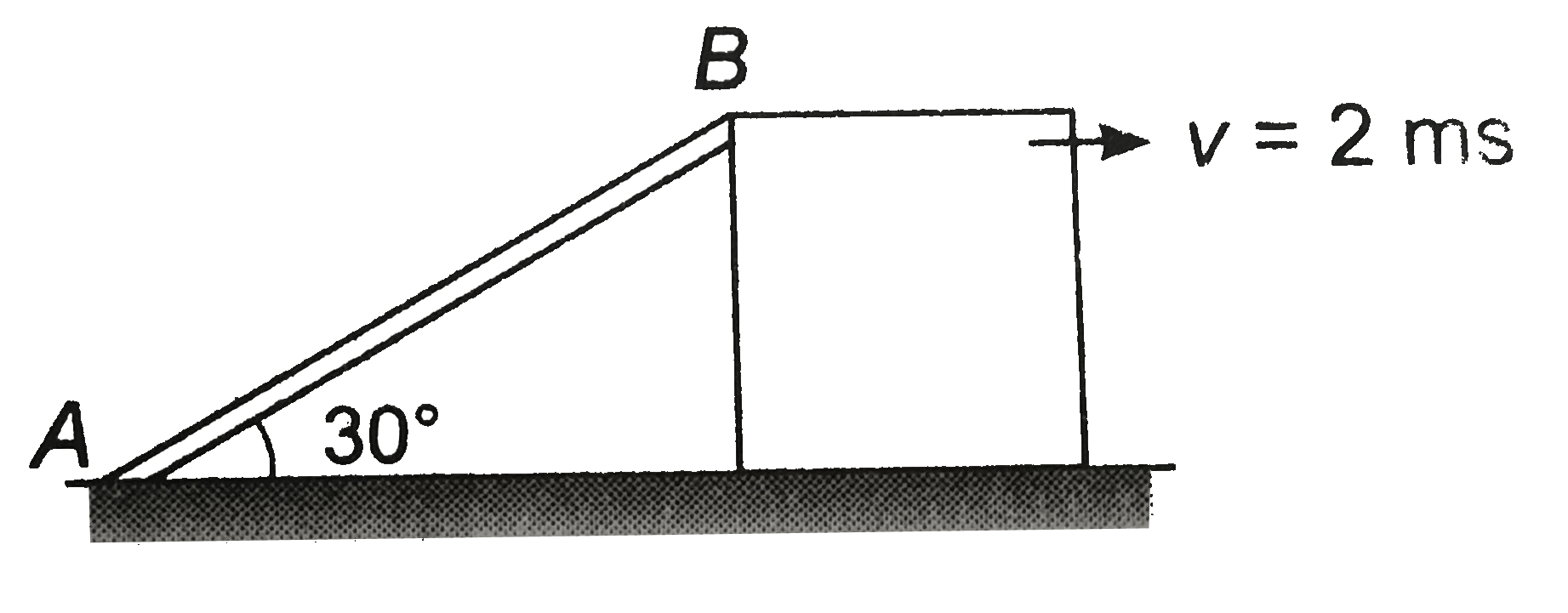
View SolutionA rod AB is shown in figure. End A of the rod is fixed on the ground. Block is moving with velocity 2ms−1 towards right. The velocity of end B of rod at the instant shown in figure is
 View Solution
View Solution

