The work done in placing a charge of on a condenser of capacity is
The correct Answer is:C
To solve the problem of calculating the work done in placing a charge of 8μC on a capacitor of capacity 100μF, we can follow these steps:
1. Convert the given values to standard units:
- The charge Q is given as 8μC. To convert microcoulombs to coulombs:
Q=8μC=8×10−6C
- The capacitance C is given as 100μF. To convert microfarads to farads:
C=100μF=100×10−6F
2. Use the formula for work done in charging a capacitor:
The work done W in charging a capacitor is given by the formula:
W=12Q2C
3. Substitute the values into the formula:
- Substitute Q and C into the formula:
W=12(8×10−6)2100×10−6
4. Calculate Q2:
- Calculate Q2:
Q2=(8×10−6)2=64×10−12C2
5. Substitute Q2 back into the work formula:
W=1264×10−12100×10−6
6. Simplify the expression:
- Divide 64×10−12 by 100×10−6:
W=12×64100×10−12+6=12×64100×10−6
- This simplifies to:
W=32100×10−6=0.32×10−6J
7. Convert to standard scientific notation:
W=3.2×10−7J
Final Answer:
The work done in placing a charge of 8μC on a capacitor of capacity 100μF is:
W=3.2×10−7 Joules
- The charge Q is given as 8μC. To convert microcoulombs to coulombs:
Q=8μC=8×10−6C
- The capacitance C is given as 100μF. To convert microfarads to farads:
C=100μF=100×10−6F
The work done W in charging a capacitor is given by the formula:
W=12Q2C
- Substitute Q and C into the formula:
W=12(8×10−6)2100×10−6
- Calculate Q2:
Q2=(8×10−6)2=64×10−12C2
W=1264×10−12100×10−6
- Divide 64×10−12 by 100×10−6:
W=12×64100×10−12+6=12×64100×10−6
- This simplifies to:
W=32100×10−6=0.32×10−6J
W=3.2×10−7J
The work done in placing a charge of 8μC on a capacitor of capacity 100μF is:
W=3.2×10−7 Joules
Topper's Solved these Questions
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP20videos
ELECTROSTATICS
- BOOK - MARVEL PUBLICATIONCHAPTER - ELECTRONS AND PHOTONS EXERCISE - TEST YOUR GRASP - 1715videos
ELECTRONS AND PHOTONS
- BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -220videos
GRAVITATION
Similar Questions
A charge of +1C is placed at the centre of a spherical shell of radius 10cm. What will be the work done in moving a charge of +1μC on its surface through a distance of 5 cm?
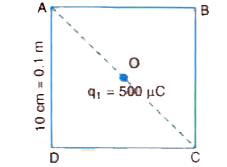
View SolutionA500μC charge is at the centre of a square of side 10 cm. Find the work done in moving a charge of 10μC between two diagonally opposite points on the square.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The work done in placing a charge of 8×10−18 coulomb on a condenser of capacity 100 micro-farad is
A(a) 16×10−32 jouleB(b) 3.1×10−26 jouleC(c) 4×10−10 jouleD(d) 32×10−32 joule - Question 2 - Select One
A condenser A of capacity 4μF has a charge 20μC and another condenser B of capacity 10μF has a charge 40μC. If they are connected parallel, then
Acharge flows from B to A till the charges on them are equalBcharge flows from B to A till common potential is reachedCcharged flows from A to B till common potential is reachedDcharge flow from A to B till charges on them are equal. - Question 3 - Select One
A dipole of 2μC charges each, consists of the positive charge at the point P (1, -1) and the negative charge is placed at the point Q(-1, 1). The work done in displacing a charge of +1μC from point A(−3,−3) to B (4, 4) is
A1.6×10−19JB3.2×10−19JCzeroD4.8eV
A circuit is shown in figure. Find the charge on the condenser having a capacity of 5μF in steady state.
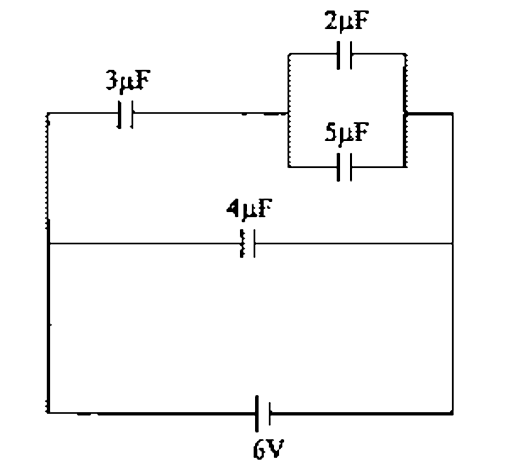 View Solution
View SolutionA charge of 10μC lies at the centre of a square. Work done in carrying a charge of 2μC from one corner of square to the diagonally opposite corner is
View SolutionThe voltage between the plates of a parallel plate condenser of capacity 2.0μF is charging at a rate of 10Vs−1. The displacement current
View Solution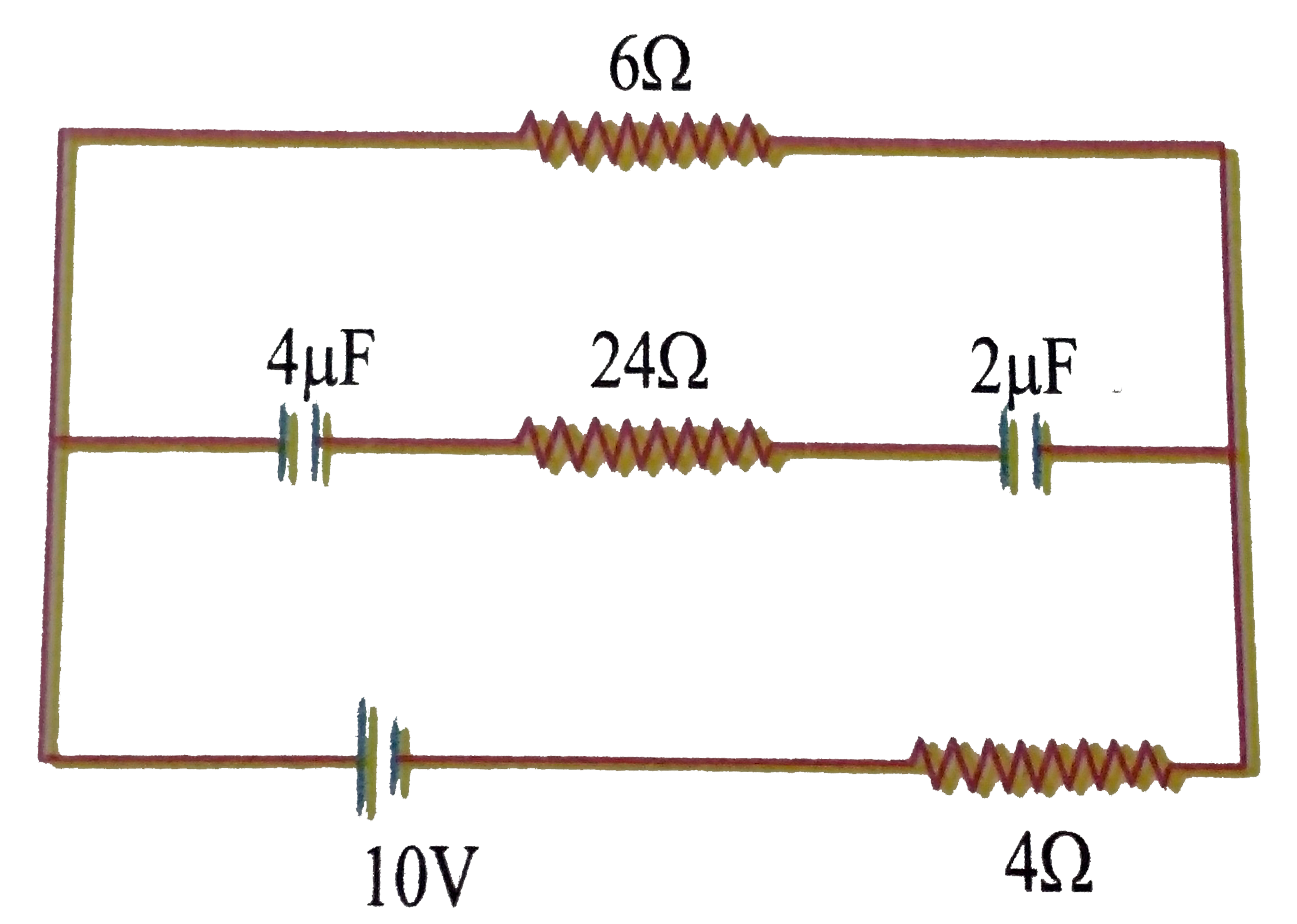
The charge developed on 4μF condenser isView SolutionA circuit is shown in the figure below. Find out the charge of the condenser having capacity 5μF
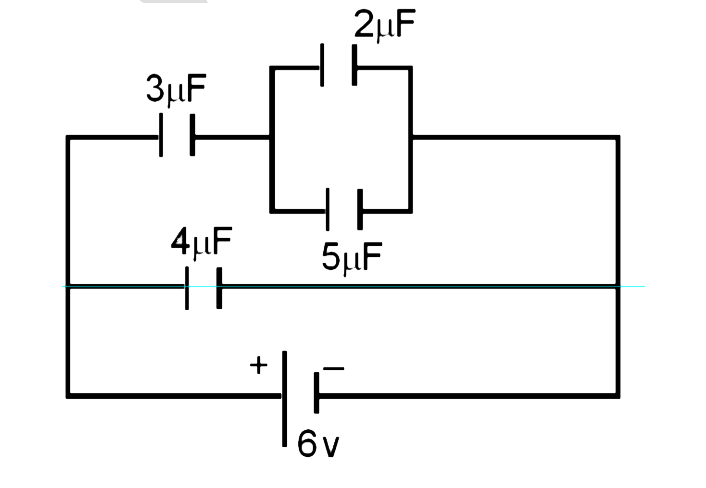 View Solution
View Solution

