There is a thin symmetric bi-convex lens with radius of curvature for its surface to be 40 cm. One surface of the lens is silvered to make it reflecting from inner side. What will be the focal length of equivalent concave mirror?

Text Solution

Verified by Experts

We can locate equivalent centre of curvature for the equivalent mirror. We know that for concave mirror image is formed on object itself if object is placed at centre of curvature of concave mirror. Let .x. be the distance of object placed in front of un-silvered surface of lens.

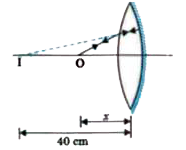
If virtual image from the refraction is formed at a distance 40 cm behind the lens then the light ray will become perpendicular to the silvered surface and then will be reflected back along the same path and the final image will be formed on the location of object.
$\frac{μ_{2}}{v} - \frac{μ_{1}}{u} = \frac{μ_{2} - μ_{1}}{R}$
$\frac{1.5}{- 40} - \frac{1}{- x} = \frac{1.5 - 1}{+ 40}$
$\Rightarrow \frac{1}{x} = \frac{0.5}{40} + \frac{1.5}{40} = \frac{2}{40}$
$\Rightarrow x = 20 c m$
Hence, image of object kept at a distance of 20 cm from this equivalent mirror will be formed on object itself hence radius of curvature for the equivalent mirror is 20 cm. We know that focal length is half of the radius of curvature and hence focal length of equivalent concave mirror will be 10 cm.
$f = - 10 c m .$

Updated on:21/07/2023

If in a plano-convex lens, the radius of curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm , then the refractive index of the material of lens will be
A1.5
B1.66
C1.33
D3
If in a plano-convex lens, the radius curvature of the convex surface is 10 cm and the focal length of the lens is 30 cm, then the refractive index of the material of lens will be
A $1.5$
B $1.66$
C $1.33$
D3
If in a plano-convex lens, the radius curvature of the convex surface is 10 cm and the focal length of the lens is 20 cm , then the refractive index of the material of lens will be
A $1.5$
B $1.66$
C $1.33$
D3