There is a uniform electrostatic field in a region. The potential at various points on a small sphere centred at P, in the region, is found to vary between in limits 589.0V to 589.8 V. What is the potential at a point on the sphere whose radius vector makes an angle of 60∘ with the direction of the field ?
589.5V
589.2V
589.4V
589.6V
The correct Answer is:C
Potential gradient is given by
ΔV=E.d
0.8−Ed (max)
ΔV=Edcosθ=0.8×cos60=0.4
Hence maximum potential at a point on the sphere =589.4V
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE -1: CONCEPT BUILDER
58 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR
24 Videos
- ELECTROMAGNETIC WAVESBOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise - 2 : Concept Applicator
30 Videos
- GRAVITATIONBOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2
30 Videos
Similar Questions
Knowledge Check
In a certain region of space a uniform and constant electric field and a magnetic field parallel to each other are present. A proton is fired from a point A in the field with speed v=4×104m/s at an angle of α with the field direction. The proton reaches a point B in the field where its velocity makes an angle β with the field direction. If sinαsinβ=√3. Find the electric potential difference between the points A and B. Take mp(mass of proton) =1.6×10−27kg and c(magnitude of electronic charge)=1.6×1019C.
A16VB16/3VC90VD30VIn a certain region of space a uniform and constant electric field and a magnetic field parallel to each other are present. A proton is fired from a point A in the field with speed V=4×104m/s at an angle of α with the field direction. The proton reaches a point B in the field where its velocity makes an angle β with the field direction. If sinαsinβ=√3. Find the electric potential difference between the points A and B. Take mp (mass of proton) =1.6×10−27kg and e (magnitude of electronic charge) =1.6×10−19C.
A16 VB40 VC90 VD30 VThe electrostatic potential for a uniformly charged conducting sphere at a point P on the surface of conductor of radius R is given by Vp=KQR. The potential at a point P at a distance r such that r<J? is
AKQrBKQRCzeroDData insufficient
A uniform electric field is along x-axis. The potential difference VA−VB=10V is between two points A (2m, 3m) and (4m, 8m). Find the electric field intensity.
View SolutionOn the basis of your understanding of the following paragraph and the related studied concepts.
An equipotential surface is a surface with a constant value of electric potential at all points on the surface. The component of electric field parallel to an equipotential surface is zero, as the potential does not change in this direction. Thus, the electric field is perpendicular to the equipotential surface at each point of the surface. Further, say the direction of electric field electrical potential gradually fall with distance.
If electric potential at origin point O be 100 V, then for electric field specified in part (b), draw equipotential surfaces corresponding to potentials 80 V, 60 V and 40 V respectively.
View Solution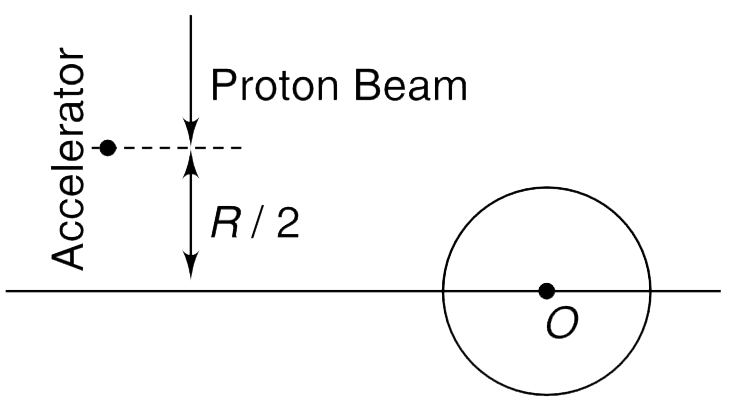
A proton accelerator produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharged distant metal sphere of radius R. The sphere is fixed and centered at point O. The initial path of the beam is at a distance of (R/2) from the centre, as indicated in the diagram. The protons in the beam that collide with the sphere get absorbed and cause it to become uniformly charged. The subsequent potential field at the accelerator due to the sphere can be neglected. Assume the mass of the proton as mP and the charge on it as e.
(a) After a long time, when the potential of the sphere reaches a constant value, sketch the trajectory of proton in the beam. (b) Once the potential of the sphere has reached its final, constant value, find the minimum speed v of a proton along its trajectory path. (c) Find the limiting electric potential of the sphere.
View SolutionA solid spherical region having a spherical cavity whose daimeter R is equal to the radius of the spherical region, has a total charge 'Q'. Find the electric field and potential at a point P as shown.

View SolutionA solid conducting sphere of radius R is placed in a uniform electric field E as showo in figure. Due to electric field non uniform surface charges are induced on the surface of the sphere. Consider a point A on the surface of sphere at a polar angle θ from the direction of electric field as shown in figure. Find the surface density of induced charges at point A in terms of electric field and polar angle θ : lt brgt

View Solution
