There is one long line charge with linear charge density λ. One electron is moving in a circular path around this line charge. Plane of the circle is perpendicular to line charge and line charge passes through centre of circle. Prove that kinetic energy of electron is independent to the radius of a circle.
To prove that the kinetic energy of an electron moving in a circular path around a long line charge with linear charge density λ is independent of the radius of the circle, we can follow these steps:
1. Identify the Electric Field due to the Line Charge:
The electric field E at a distance r from an infinite line charge with linear charge density λ is given by:
E=2kλr
where k is Coulomb's constant, k=14πϵ0.
2. Determine the Electric Force on the Electron:
The force Fe acting on the electron (which has charge −e) due to the electric field is:
Fe=−eE=−e(2kλr)=−2keλr
The negative sign indicates that the force is attractive, pulling the electron towards the line charge.
3. Relate the Electric Force to the Centripetal Force:
For the electron to move in a circular path, the electric force must provide the necessary centripetal force Fc:
Fc=mev2r
where me is the mass of the electron and v is its velocity.
4. Set the Electric Force Equal to the Centripetal Force:
Equating the magnitudes of the electric force and the centripetal force gives:
mev2r=2keλr
We can cancel r from both sides (assuming r≠0):
mev2=2keλ
5. Calculate the Kinetic Energy:
The kinetic energy K of the electron is given by:
K=12mev2
Substituting the expression for mev2 from the previous step:
K=12(2keλ)=keλ
6. Conclusion:
The kinetic energy of the electron is:
K=keλ
This expression shows that the kinetic energy K is dependent only on the charge density λ and the charge of the electron e, and is independent of the radius r of the circular path.
The electric field E at a distance r from an infinite line charge with linear charge density λ is given by:
E=2kλr
where k is Coulomb's constant, k=14πϵ0.
The force Fe acting on the electron (which has charge −e) due to the electric field is:
Fe=−eE=−e(2kλr)=−2keλr
The negative sign indicates that the force is attractive, pulling the electron towards the line charge.
For the electron to move in a circular path, the electric force must provide the necessary centripetal force Fc:
Fc=mev2r
where me is the mass of the electron and v is its velocity.
Equating the magnitudes of the electric force and the centripetal force gives:
mev2r=2keλr
We can cancel r from both sides (assuming r≠0):
mev2=2keλ
The kinetic energy K of the electron is given by:
K=12mev2
Substituting the expression for mev2 from the previous step:
K=12(2keλ)=keλ
The kinetic energy of the electron is:
K=keλ
This expression shows that the kinetic energy K is dependent only on the charge density λ and the charge of the electron e, and is independent of the radius r of the circular path.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Practice Problems
88 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - MODERN PUBLICATIONCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - Conceptual Questions
51 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
14 Videos
Similar Questions
A long cylindrical wire carries a positive charge of linear density 2.0 xxx 10^(-8) C m^(-1). An electron revolves around it in a circular path under the influence of the attactive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
View SolutionA long cylindrical wire carries a positive charge of linear density λ. An electron (−e,m) revolves around it in a circular path under the influence of the attractive electrostatic force. Find the speed of the electron.
View Solution
Knowledge Check
When an electron moves in a circular path around a stationay nucles charge at the center
Athe acceleration of the electron changesBthe velocity of the electon changeCelectric field due to the nucleus at the electron changesDnone of theseThere is a line charge of infinite length with positive charge distributed uniformly along ita length. One electron is moving in a circular path with the plane of the circle perpendicular to the line charge.
AKinetic energy of the electron is independent of its distance from line chargeBTime taken by charged particle to complete one full circle around line charge is directly proportional to its distance from the line chargeCSquare of the time taken to complete one circle is proportional to the third power of its distance from the line charge.DElectric field intensity at a point due to line charge in inversely proportional to the length of perpendicular drawn from point on line charge.For an infinite line of charge having linear charge density λ lying along x-axis the work done in moving a charge q form C to A along CA is
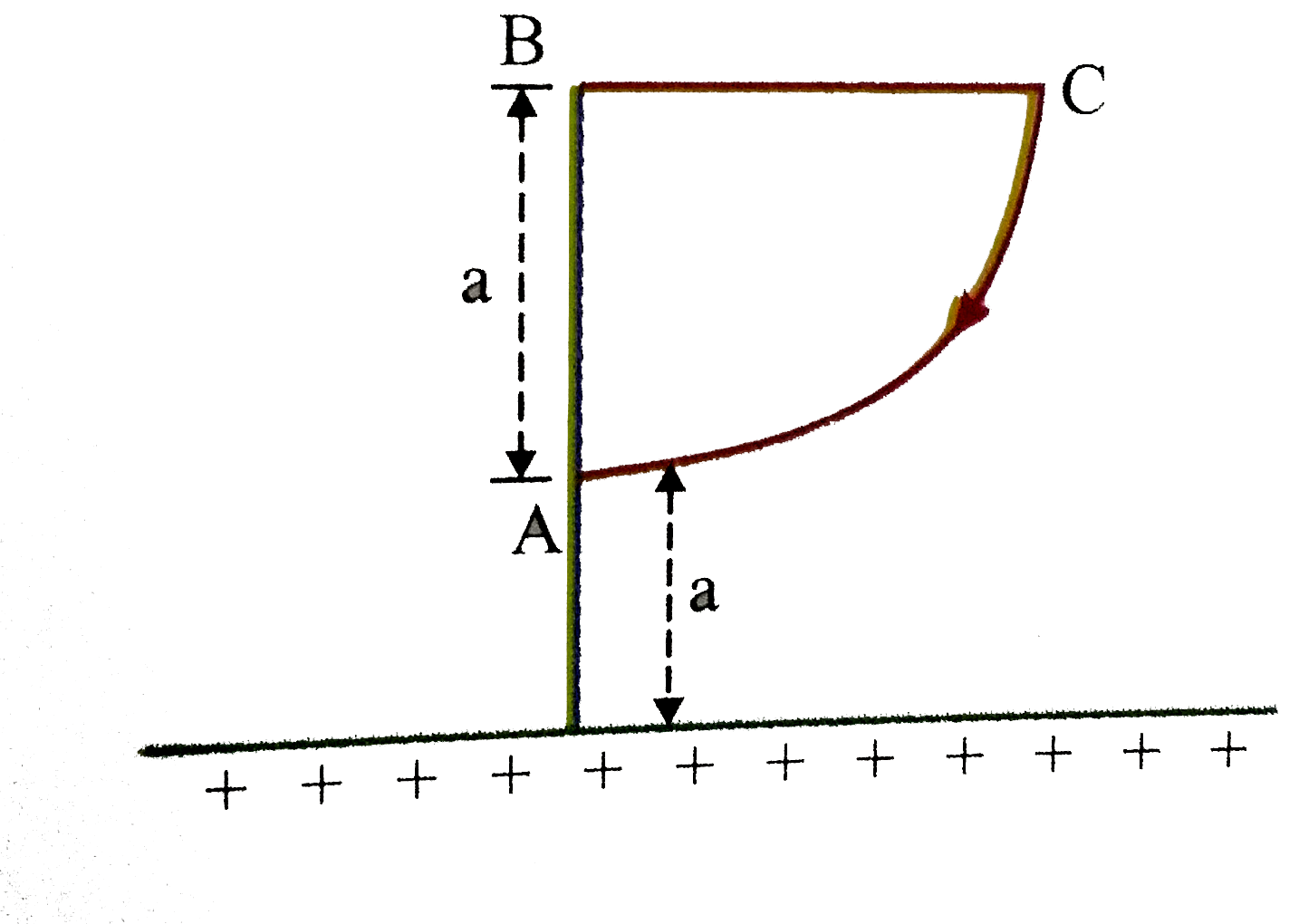 Aqλ2πε0In2Bqλ2πε0In√2Cqλ4πε0In2Dqλ2πε0In(0.5)
Aqλ2πε0In2Bqλ2πε0In√2Cqλ4πε0In2Dqλ2πε0In(0.5)
Consider a very long plastic wire with charge density λ .Flux passing through a circle of radius R having centre at one of ends of wire is
View SolutionAn infinitely long time charge has linear charge density λC/m the line charge is along the line x=0,z=2m find the electric field at point (1,1,1) m.
View SolutionA charge moves with a speed v in a circular path of radius r around a long uniformly charged conductor.
View SolutionA charge moves in a circle perpendicular to a magnetic field. The time period of revolution is independent of
View SolutionTwo parallel infinite line charges with linear charge densities +λC/m and −λ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
View Solution
