Three capacitors each of 3μF, are provided. These cannot be combined to provide the resultant capacitance of
1μF
2μF
4.5μF
6μF
The correct Answer is:D
To solve the problem of determining which resultant capacitance cannot be achieved using three capacitors of 3 µF each, we will analyze the possible combinations of these capacitors in series and parallel.
1. Understanding Capacitance Combinations:
- Capacitors can be combined in two main ways: series and parallel.
- In series, the total capacitance C is given by:
1C=1C1+1C2+1C3
- In parallel, the total capacitance C is given by:
C=C1+C2+C3
2. Calculating Series Combination:
- For three capacitors each of 3μF:
1C=13+13+13=33=1
C=1μF
3. Calculating Parallel Combination:
- For the same three capacitors in parallel:
C=3+3+3=9μF
4. Mixed Combinations:
- Two in Parallel and One in Series:
- Combine two capacitors in parallel:
Cp=3+3=6μF
- Then, combine this with the third capacitor in series:
1C=16+13
- Finding a common denominator (6):
1C=16+26=36=12
C=2μF
- Two in Series and One in Parallel:
- Combine two capacitors in series:
1Cs=13+13=23⟹Cs=1.5μF
- Then, combine this with the third capacitor in parallel:
Ctotal=1.5+3=4.5μF
5. Summary of Possible Resultant Capacitances:
- From the calculations, we have the following possible resultant capacitances:
- 1μF (all in series)
- 2μF (two in parallel, one in series)
- 4.5μF (two in series, one in parallel)
- 9μF (all in parallel)
6. Identifying the Impossible Resultant Capacitance:
- The question asks for the resultant capacitance that cannot be achieved. The possible capacitances are 1μF,2μF,4.5μF, and 9μF.
- The capacitance 6μF cannot be achieved with any combination of the three capacitors.
Final Answer:
The resultant capacitance that cannot be provided by combining three capacitors of 3μF each is 6 µF.
- Capacitors can be combined in two main ways: series and parallel.
- In series, the total capacitance C is given by:
1C=1C1+1C2+1C3
- In parallel, the total capacitance C is given by:
C=C1+C2+C3
- For three capacitors each of 3μF:
1C=13+13+13=33=1
C=1μF
- For the same three capacitors in parallel:
C=3+3+3=9μF
- Two in Parallel and One in Series:
- Combine two capacitors in parallel:
Cp=3+3=6μF
- Then, combine this with the third capacitor in series:
1C=16+13
- Finding a common denominator (6):
1C=16+26=36=12
C=2μF
- Combine two capacitors in series:
1Cs=13+13=23⟹Cs=1.5μF
- Then, combine this with the third capacitor in parallel:
Ctotal=1.5+3=4.5μF
- From the calculations, we have the following possible resultant capacitances:
- 1μF (all in series)
- 2μF (two in parallel, one in series)
- 4.5μF (two in series, one in parallel)
- 9μF (all in parallel)
- The question asks for the resultant capacitance that cannot be achieved. The possible capacitances are 1μF,2μF,4.5μF, and 9μF.
- The capacitance 6μF cannot be achieved with any combination of the three capacitors.
The resultant capacitance that cannot be provided by combining three capacitors of 3μF each is 6 µF.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE -1: CONCEPT BUILDER
58 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR
24 Videos
- ELECTROMAGNETIC WAVESBOOK - DISHA PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise - 2 : Concept Applicator
30 Videos
- GRAVITATIONBOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2
30 Videos
Similar Questions
Three capacitors each of capacitance 9 pF are connected in series.
(a) What is the total capacitance of the combination ?
(b) What is the potential difference across each capacitor if the combination is connected to a 120 V supply ?
View SolutionFive capacitors each of capacitance 20μF are joined as shown in the figure. The equivalent capacitance between A and C is

View Solution
Knowledge Check
Three capacitors each of capacity 4μF are to be connected in such a way that the effective capacitance is 6μF. This can be done by
AConnecting them in parallelBConnecting two in series and one in parallelCConnecting two in parallel and one in seriesDConnecting all of them in seriesThree capacitors 2μF,3,μFand6μF are joined'in series with each other.
The equivalent capacitance is:A12μFB1μFC2μFD11μFTwo condensers each of 4μF capacitance are joined in parallel. The resultant capacitance of the combination is
A2μFB4μFC6μFD8μF
We are provided 10 capacitors each of 1μF capacitance. We can employ them so as to have a minimum capacitance of 0.1μF and maximum capacitance of 10μF.
View SolutionSome capacitors each of capacitance 30μF are connected as shown in. Calculate the equivalent capacitance between terminals A and B
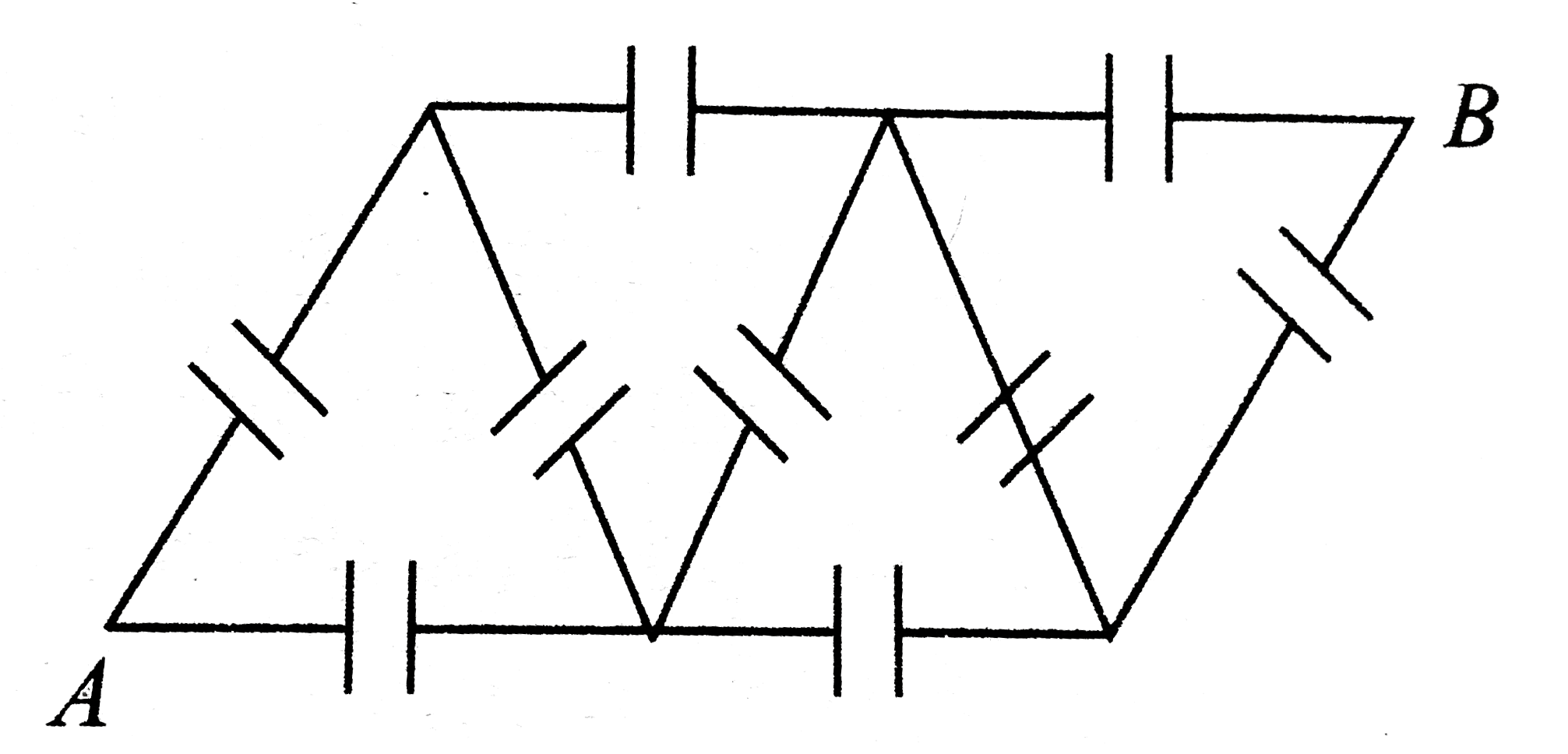 .
.
View SolutionThree capacitors each of capacitance 1μF are connected in parallel.To this combination,a fourth capacitor of capacitance 1μFis connected in series.The resultant capacitance of the system
View SolutionThree capacitors each of capacitance 1μF are connected in parallel. To this combination, a fourth capacitor capacitance 1μF is connected in series. The resultant capacitance of the system is
View SolutionIf three capacitors each of capacity 1μF are connected in such a way that the resultant capacity is 1.5μF, then
View Solution
