Three point charges are placed at the vertices of an equilateral triangle ABC of side l. If these charges are displaced at the find points respectively, find the amount of work done in shifting the charges to their new positions.
To find the amount of work done in shifting the charges +Q,+2Q, and −3Q from points A,B,C to new positions A1,B1,C1 respectively, we need to calculate the initial and final potential energies of the system and then determine the work done based on the change in potential energy.
Step 1: Calculate the Initial Potential Energy
The initial potential energy Ui of the system can be calculated using the formula for the potential energy between point charges:
Ui=k∑i<jqiqjrij
Where:
- k=14πϵ0
- rij is the distance between charges qi and qj.
For the charges at the vertices of an equilateral triangle with side length l:
1. Between +Q and −3Q:
UAC=kQ⋅(−3Q)l=−3Q2kl
2. Between +Q and +2Q:
UAB=kQ⋅2Ql=2Q2kl
3. Between +2Q and −3Q:
UBC=k2Q⋅(−3Q)l=−6Q2kl
Now, summing these potential energies gives:
Ui=−3Q2kl+2Q2kl−6Q2kl=−7Q2kl
Step 2: Calculate the Final Potential Energy
After displacing the charges to new positions A1,B1,C1, which form a smaller equilateral triangle with side length l2:
1. Between +Q and −3Q:
UA1C1=kQ⋅(−3Q)l2=−6Q2kl
2. Between +Q and +2Q:
UA1B1=kQ⋅2Ql2=4Q2kl
3. Between +2Q and −3Q:
UB1C1=k2Q⋅(−3Q)l2=−12Q2kl
Now, summing these potential energies gives:
Uf=−6Q2kl+4Q2kl−12Q2kl=−14Q2kl
Step 3: Calculate the Work Done
The work done W in moving the charges is given by the change in potential energy:
W=Uf−Ui
Substituting the values we calculated:
W=(−14Q2kl)−(−7Q2kl)=−14Q2kl+7Q2kl=−7Q2kl
Final Result
Thus, the amount of work done in shifting the charges to their new positions is:
W=−7Q24πϵ0l
- k=14πϵ0
- rij is the distance between charges qi and qj.
UAC=kQ⋅(−3Q)l=−3Q2kl
UAB=kQ⋅2Ql=2Q2kl
UBC=k2Q⋅(−3Q)l=−6Q2kl
Ui=−3Q2kl+2Q2kl−6Q2kl=−7Q2kl
UA1C1=kQ⋅(−3Q)l2=−6Q2kl
UA1B1=kQ⋅2Ql2=4Q2kl
UB1C1=k2Q⋅(−3Q)l2=−12Q2kl
Uf=−6Q2kl+4Q2kl−12Q2kl=−14Q2kl
Substituting the values we calculated:
W=(−14Q2kl)−(−7Q2kl)=−14Q2kl+7Q2kl=−7Q2kl
Similar Questions
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View SolutionElectric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
View Solution
Knowledge Check
Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
Athe field is zero but potential is nonzero.Bthe field is nonzero but potential is zero.Cboth field and potential are zero.Dboth field and potential are nonzero.Three positive charges of equal magnitude q are placed at the vertices of and equilateral triangle of side l. How can the system of charges be placed in equilibrium?
Aby placing a charge Q=−q/√3 at the centroid of the triangleBby placing a charge Q=q/√3 at the centroid of the triangleCby placing a charge Q=q at the centroid of the triangleDby placing a charge Q=−q at the centroid of the triangleThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
A(√34πε0)(qa)2B(√24πε0)(qa)2C(√34πε0)(q2a)2D(√24πε0)(2qa)2
Three points charges =q, -2q, +q are arranged on the vertices of an equilaterial triangle as shown in the figure. Find he dipole moment of the system.
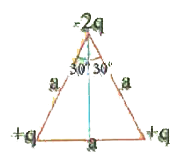
View SolutionThree charges q1=1μC,q2=2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. Find the net electric force acting on charge q1

View SolutionEqual charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
View SolutionElectric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
View SolutionThree point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is
View Solution
