Three point masses each of mass m rotate in a circle of radius r with constant angular velocity ω due to their mutual gravitational attraction. If at any instant, the masses are on the vertices of an equilateral triangle of side a, then the value of ω is
√(Gma3)
√(3GMa3)
√(Gm3a3)
None
The correct Answer is:B
Here, F0=Gm2a2
∴F=2F0cos30∘=2Gm2a2√32

=√3Gm2a2 or mrω2=√3Gm2a2
or ma√3ω2=√3Gm2a2∴ω=√(3Gma3)
Topper's Solved these Questions
Similar Questions
Two particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionFour particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
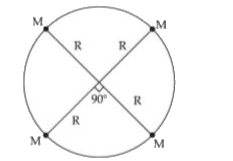 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2) - Question 2 - Select One
The gravitational potential energy of a system of three particles of mass m each kept at the vertices of equilateral triangle of side x will be
A−Gm2xB−Gm23xC−3Gm2xD3Gm2x2 - Question 3 - Select One
Two particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
A12√GmRB√4GMRC12R√1GmD√Gm2R
_S01_003_Q01.png)
Two particles of equal mass (m) each move in a circle of radius (r) under the action of their mutual gravitational attraction find the speed of each particle.View SolutionTwo particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionTwo particles of mass m1 and m2, approach each other due to their mutual gravitational attraction only. Then
View SolutionA stone of mass M is tied at the end of a string, is moving in a circle of radius R, with a constant angular velocity ω. The total work done on the stone, in any half circle, is:
View Solution

