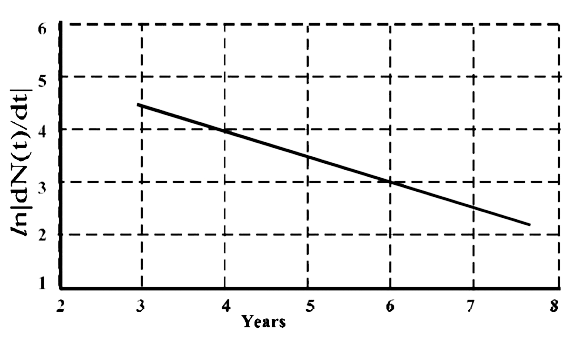
To determine the half life of a radioactive element , a student plot a graph of in $∣ ∣ ∣ \frac{d N (t)}{d t} ∣ ∣ ∣$ versus $t$ , Here $∣ ∣ ∣ \frac{d N (t)}{d t} ∣ ∣ ∣$ is the rate of radioactive decay at time t , if the number of radioactive nuclei of this element decreases by a factor of p after $4.16$ year the value of p is

Video Solution

Text Solution

Verified by Experts

The correct Answer is:8

Updated on:21/07/2023

The $t_{0.5}$ of a radioactive element is related to its average life by the expression
A $T_{12} = 1.44 T_{a v}$
B $T_{12} = 1.36 T_{a v}$
C $T_{12} = 0.693 T_{a v}$
D $T_{12} = \frac{T_{a v}}{0.693}$
The half life of a radioactive element is T and its initial activity at $t = 0$ is $A_{0}$ and at $t = t$ it is A, then
A $A = A_{0} 2^{t / T}$
B $A = A_{0} {(2 t)}^{T}$
C $A_{0} = A 2^{t / T}$
D $A_{0} = A 2^{- t / T}$
The half life of a radioactive substance is $T_{0}$ . At $t = 0$ ,the number of active nuclei are $N_{0}$ . Select the correct alternative.
AThe number of nuclei decayed in time internal $0 - t$ is $N_{0} e^{- λ t}$
BThe number of nuclei decays in time interval $0 - t$ is $N_{0} (1 - e^{- λ t})$
CThe probability that a radioactive nuclei does not decay in interval $0 - t$ is $e^{- λ t}$
DThe probability that a radioactive nuclei does not decay in interval $1 - e^{- λ t}$