Two blocks 1 and 2, each having mass m, are placed on a smooth table connected to three identical springs as shown in the figure. Each spring has a force constant K. Initially, all springs are relaxed. The system is disturbed and starts moving. Let x1 and x2 represent the displacements of the two blocks from their respective mean positions.
(a) Prove that the quantity A=x1+x2 varies sinusoidally and calculate its angular frequency wa.
(b) Prove that the quantity B=x1−x2 varies sinusoidally and calculate its angular frequency wb.
(c) Prove that motion of block 1 is superposition of two SHMs. Write frequency of the component SHMs.

The correct Answer is:(a) ωa=√km
(b)ωb=√3km
(c)ωa and ωb
Topper's Solved these Questions
Similar Questions
Two identical blocks 1 and 2, each of mass m, are kept on a smooth horizontal surface, connected to three springs as shown in the figure. Each spring has a force constant k. Under suitable initial conditions, the two blocks oscillate in phase and their respective displacement from the mean position is given by
x1=Asinωt and x2=Asinωt
(i) Suggest one such initial condition that will result in such oscillation.
(ii) Find ω

View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be

View Solution
Knowledge Check
As shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be
 Ak1k2Bk1+k2C1k1+1k2Dk1k2k1+k2
Ak1k2Bk1+k2C1k1+1k2Dk1k2k1+k2A block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
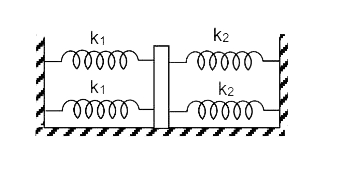 A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m
A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)mA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.
 A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
A√k1+k2mxB√k1k2m(k1+k2)xC ⎷k21k22m(k21+k22)xD ⎷k31k32m(k31+k32)
Two blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ?
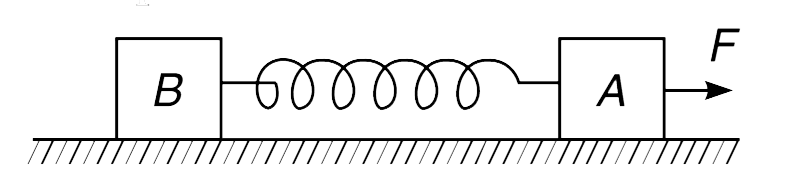
View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it psses through the mean position shown.

View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

View SolutionA block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :

View SolutionA block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-

View Solution
