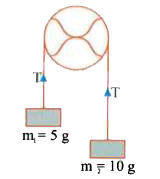
Two blocks and are hung vertically over a light frictionless pulley as shown in the figure. What is the acceleration of the masses when left free?

(where g is acceleration due to gravity)
The correct Answer is:A

For the system of the two masses . Hence moves downwards and moves upwards.
Their common accleration is given by
Topper's Solved these Questions
Similar Questions
Two blocks m1 = 5 g and m2= 10 g are hung vertically over a light frictionless pulley as shown in figure. What is the acceleration of the masses when left free ?
 View Solution
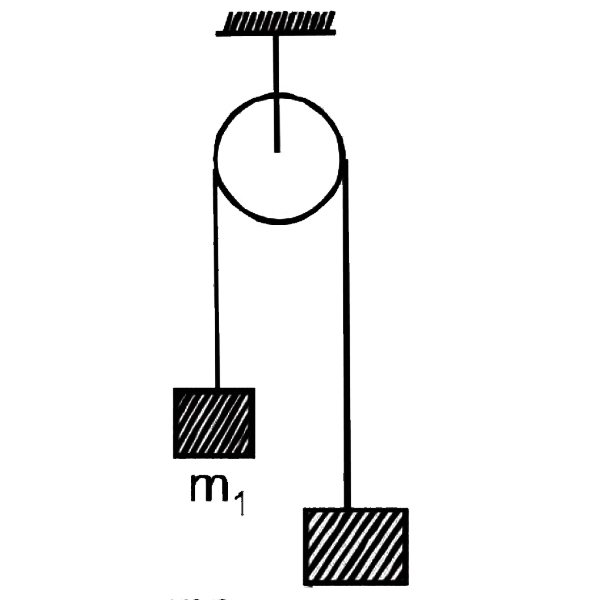
View SolutionTwo masses m1=5kg and m2=4.8kg tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when left free to move?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two masses m1=5kg and m2=4.8kg tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when left free to move?
 A(a) 5m/s2B(b) 9.8m/s2C(c) 0.2m/s2D(d) 4.8m/s2
A(a) 5m/s2B(b) 9.8m/s2C(c) 0.2m/s2D(d) 4.8m/s2 - Question 2 - Select One
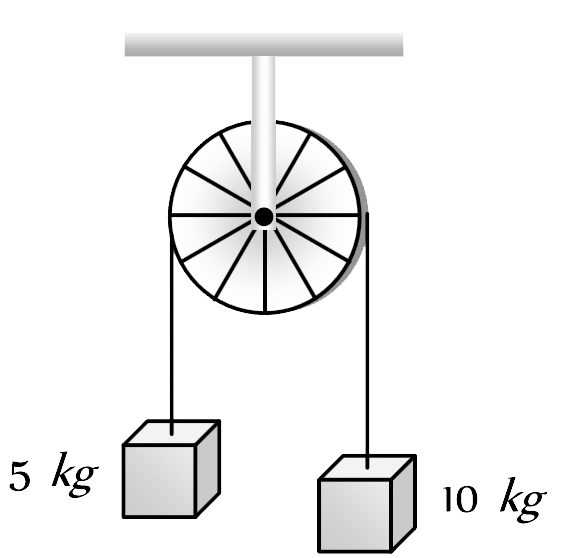
USS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
 AgBg4C4g9D5g9
AgBg4C4g9D5g9 - Question 3 - Select One
USS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
 AgBg2Cg3Dg4
AgBg2Cg3Dg4
Two masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :
 View Solution
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :
 View Solution
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :
 View Solution
View SolutionUSS 150) Two masses of 5 kg and 10 kg are connected to a pulley as shown. What will be the acceleration of the system (g= acceleration due to gravity)
 View Solution
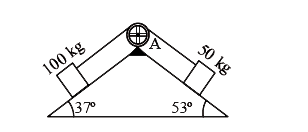
View SolutionTwo blocks are connected by a cord passing over a small frictionless pulley and resting on frictionless planes as shown in the figure. The acceleration of the blocks is :
 View Solution
View Solution

