Two bodies A and B carry charges −3.00μC and −0.44μC. How many that they acquire equal charges?
To solve the problem of how many charges need to be transferred from body A to body B so that they acquire equal charges, we can follow these steps:
1. Identify the Initial Charges:
- Let the charge on body A (Q1) be -3.00 µC.
- Let the charge on body B (Q2) be -0.44 µC.
2. Define the Charge Transfer:
- Let n be the number of electrons transferred from A to B.
- The charge of one electron (e) is approximately 1.6×10−19 coulombs.
3. Calculate the Total Charge After Transfer:
- After transferring n electrons, the charge on body A will be:
Q1′=Q1+n⋅e=−3.00μC+n⋅(1.6×10−6C)
- The charge on body B will be:
Q2′=Q2−n⋅e=−0.44μC−n⋅(1.6×10−6C)
4. Set the Charges Equal:
- To find n, we set the charges equal to each other:
Q1′=Q2′
- This gives us:
−3.00μC+n⋅(1.6×10−6C)=−0.44μC−n⋅(1.6×10−6C)
5. Rearranging the Equation:
- Rearranging the equation, we get:
−3.00+0.44=2n⋅(1.6×10−6)
- Simplifying gives:
−2.56=2n⋅(1.6×10−6)
6. Solving for n:
- Now, isolate n:
n=−2.562⋅(1.6×10−6)
- Calculate n:
n=−2.563.2×10−6=−800000 (approximately)
7. Convert to Electrons:
- Since we are looking for the number of electrons, we take the absolute value:
n≈8×1012 electrons
Final Answer:
To make the charges equal, approximately 8×1012 electrons must be transferred from body A to body B.
- Let the charge on body A (Q1) be -3.00 µC.
- Let the charge on body B (Q2) be -0.44 µC.
- Let n be the number of electrons transferred from A to B.
- The charge of one electron (e) is approximately 1.6×10−19 coulombs.
- After transferring n electrons, the charge on body A will be:
Q1′=Q1+n⋅e=−3.00μC+n⋅(1.6×10−6C)
- The charge on body B will be:
Q2′=Q2−n⋅e=−0.44μC−n⋅(1.6×10−6C)
- To find n, we set the charges equal to each other:
Q1′=Q2′
- This gives us:
−3.00μC+n⋅(1.6×10−6C)=−0.44μC−n⋅(1.6×10−6C)
- Rearranging the equation, we get:
−3.00+0.44=2n⋅(1.6×10−6)
- Simplifying gives:
−2.56=2n⋅(1.6×10−6)
- Now, isolate n:
n=−2.562⋅(1.6×10−6)
- Calculate n:
n=−2.563.2×10−6=−800000 (approximately)
- Since we are looking for the number of electrons, we take the absolute value:
n≈8×1012 electrons
To make the charges equal, approximately 8×1012 electrons must be transferred from body A to body B.
Similar Questions
Two charges +0.4μC and−0.2μC are placed on adjacent vertices of a square of side 10 cm. Another charge of 1.2μC is placed at the centre af the square Calculate the force and its direction in the charge kept in the centre .
View SolutionTwo tiny spheres carrying charges 1.5μCand2.5μC are located 30 cm apart. Find the potential and electric field:
(a) at the mid-point of the line joining the two charges, and
(b) at a point 10 cm from this mid-point in a plane normal to the line and passing through the mid point.
View Solution
Knowledge Check
Two bodies X and Y carry charges −6.6μC and −5μC. How many electrons should be transferred from X to Y so that they acquire equal charges?
A2X1012B5X1013C5X1012D2X1013The left most capacitor is uncharged. The other tow capacitors carry charges q1=8μCandq2=10μC . Now switch S is closed. Find the final charge on left most capacitor.
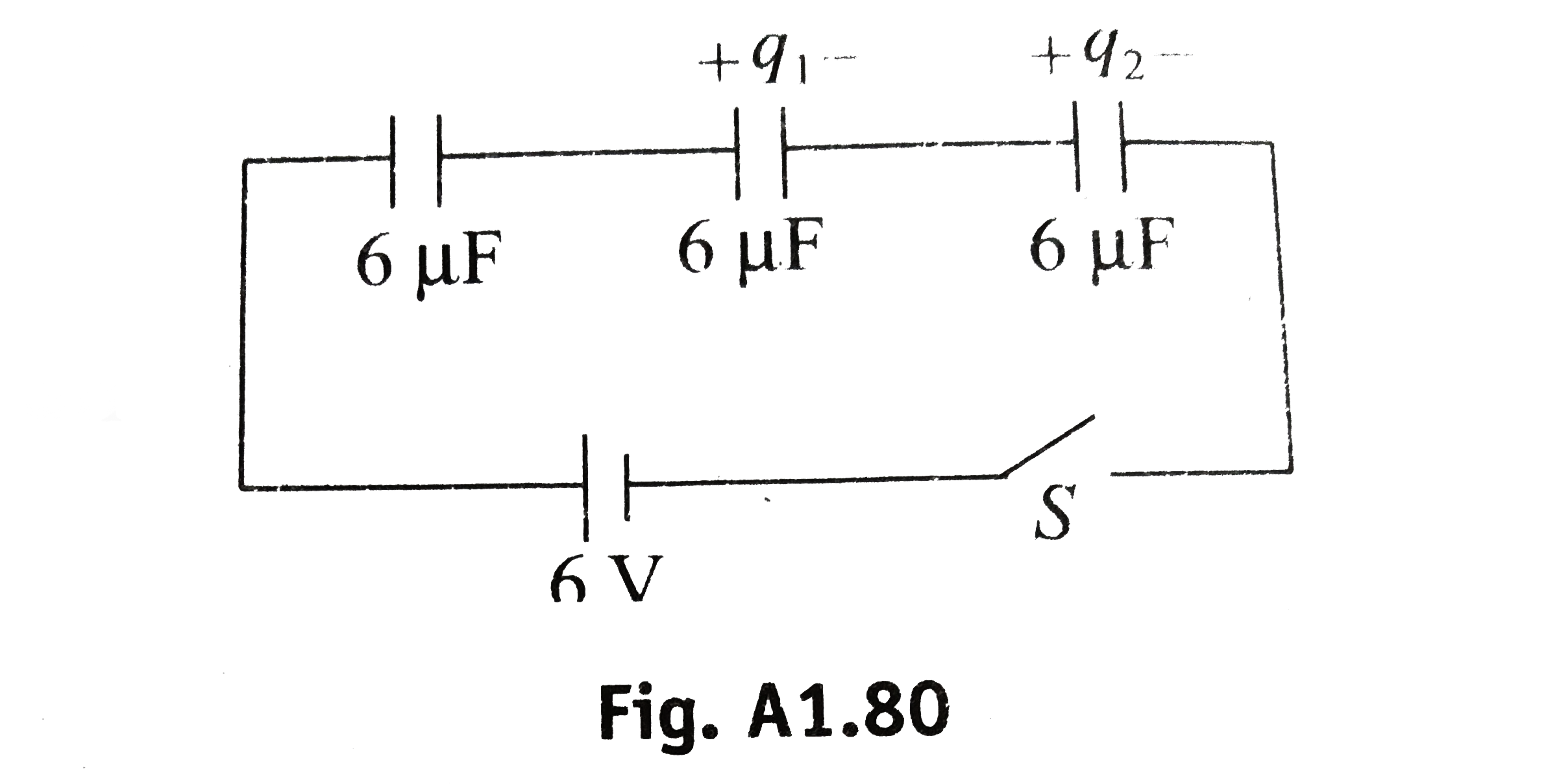 A3μCB6μCC12μCD18μC
A3μCB6μCC12μCD18μCTwo identical bodies in which charges are 40μC and −20μC. They are some distance apart. Now they are touched and kept at the same distance. The ratio of the initial to the final force between them is
A8:1B4:1C1:8D1:1
Two tiny spheres carrying charges 1.5μC and 2.5μC are located 30 cm apart. Find the potential
(a) at the mid-point of the line joining the two charges and
(b). At a point 10 cm from this mid-point in a plane normal to the line and passing through the mid-point.
View SolutionTwo point charges 10μCand−10μC are separated by a distance of 40 cm in air.
Draw an equipotential surface of the system.
View SolutionWhen two bodies A and B are rubbed, they acquire charge by frication, If the charge on positive, then the charge on B is _______.
View SolutionTwo spheres A and B of radius 4 cm and 6 cm are given charges of 80μCand40μC, respectively. If they are connected by a fine wire, then the amount of charge flowing from one to the other is
View SolutionTwo point charges +10 muC and +20 muC repel each other with a force of 100N. If a charge of-2 muC is added to each charge, then force between them will become
View Solution
