Two bodies one held 30 cm directly above the other are relased simultaneously and fall freely under gravity. After 2 sec their relative separation will be :
10 cm
20 cm
30 cm
zero
The correct Answer is:C
To solve the problem of finding the relative separation between two bodies falling freely under gravity after 2 seconds, we can follow these steps:
1. Understanding the Initial Setup:
- We have two bodies: Body A is held 30 cm above Body B.
- Both bodies are released simultaneously and fall freely under the influence of gravity.
2. Initial Separation:
- The initial separation between the two bodies is 30 cm (0.3 meters).
3. Equations of Motion:
- Since both bodies are falling freely under gravity, we can use the equation of motion:
S=ut+12at2
- Where:
- S is the distance fallen,
- u is the initial velocity (which is 0 since they are dropped),
- a is the acceleration due to gravity (approximately 9.8m/s2),
- t is the time in seconds.
4. Calculating the Distance Fallen by Each Body:
- For both bodies, since they are dropped from rest, the initial velocity u=0.
- The distance fallen by each body after t=2 seconds can be calculated as follows:
S=0+12gt2
- Substituting g=9.8m/s2 and t=2s:
S=12×9.8×(2)2=12×9.8×4=19.6m
5. Distance Fallen by Each Body:
- Both Body A and Body B fall the same distance of 19.6 meters after 2 seconds.
6. Finding the Relative Separation:
- Initially, the separation was 30 cm (0.3 m).
- After 2 seconds, both bodies have fallen the same distance (19.6 m).
- Therefore, the relative separation remains unchanged:
Relative Separation=Initial Separation=30cm(0.3m)
Final Answer:
The relative separation between the two bodies after 2 seconds is 30 cm.
- We have two bodies: Body A is held 30 cm above Body B.
- Both bodies are released simultaneously and fall freely under the influence of gravity.
- The initial separation between the two bodies is 30 cm (0.3 meters).
- Since both bodies are falling freely under gravity, we can use the equation of motion:
S=ut+12at2
- Where:
- S is the distance fallen,
- u is the initial velocity (which is 0 since they are dropped),
- a is the acceleration due to gravity (approximately 9.8m/s2),
- t is the time in seconds.
- For both bodies, since they are dropped from rest, the initial velocity u=0.
- The distance fallen by each body after t=2 seconds can be calculated as follows:
S=0+12gt2
- Substituting g=9.8m/s2 and t=2s:
S=12×9.8×(2)2=12×9.8×4=19.6m
- Both Body A and Body B fall the same distance of 19.6 meters after 2 seconds.
- Initially, the separation was 30 cm (0.3 m).
- After 2 seconds, both bodies have fallen the same distance (19.6 m).
- Therefore, the relative separation remains unchanged:
Relative Separation=Initial Separation=30cm(0.3m)
The relative separation between the two bodies after 2 seconds is 30 cm.
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - More than one choice is correct16videos
MOTION IN A STRAIGHT LINE
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion Reason12videos
MOTION IN A STRAIGHT LINE
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problems and Practice16videos
MOTION IN A STRAIGHT LINE
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type11videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - All Questions210videos
MOTION IN TWO AND THREE DIMENSIONS
Similar Questions
Two equal masses are held at a distance of 3.0cm in a line and released simulataneously. What will be the separation between them after 2s?
View SolutionIn the last question, the two particles A and B are initially held at a distance r=qQ2π∈0mu2 apart. Particle B is projected directly towards A with velocity u and particle A is released simultaneously. Find the velocity of particle A after a long time. Consider coulomb force only.
View Solution
Knowledge Check
- Question 1 - Select One
Two bodies are held separated by 9.8m vertically one above the other. They are released simultaneously to fall freely under gravity. After 2 s the relative distance between them is
A4.9mB19.6mC9.8mD392m - Question 2 - Select One
Two bodies having masses in the ratio 2:3 fall freely under gravity from heights 9:16. The ratio of their linear momenta on touching, the ground is
A2:9B3:16C1:2D3:2 - Question 3 - Select One
Two bodies having masses in the ratio 2:3 fall freely under gravity from heights 9:16. The ratio of their linear momenta on touching, the ground is
A2:9B3:16C1:2D3:2
A solid cyinder of mass m=4kg and radius R=10cm has two ropes wrapped around it. one near each end. The cylinder is held horizontally by fixing the two free ends of the cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the linear acceleration of the cylinder.
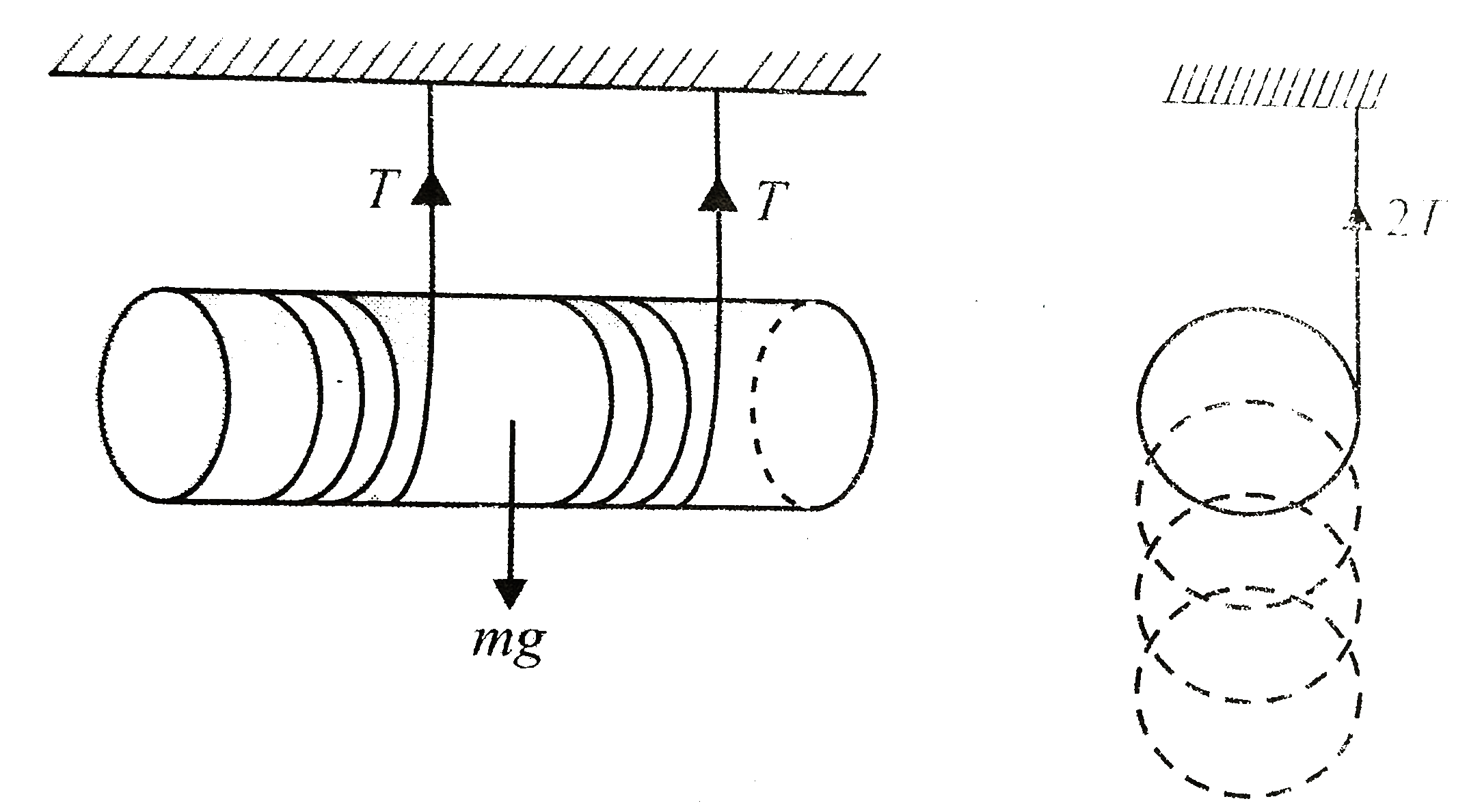 View Solution
View SolutionTwo spherical bobs, one metallic and the other of glass, of the same size are allowed to fall freely from the same height above the ground. Which of the two would reach earlier and why?
View SolutionTwo spherical bobs, one metallic and other of glass, of the same size are allowed to fall freely from the same height above the ground. Which of the two would reach the ground earlier and why ?
View SolutionTwo point masses m and M are held at rest at a large distance from each other. When released, they begin moving under their mutual gravitational pull.Find their relative acceleration (a) when separation between them becomes x.Integrate the expression of a obtained above to calculate the relative velocity of the two masses when their paration is x. Write the velocity of centre of mass of the system when separation between them is x.
View SolutionA solid cylinder of mass m=4kg and radius R=10cm has two ropes wrapped around it, one near each end. The cylinder is held horizontally by fixing the two free ends of he cords to the hooks on the ceiling such that both the cords are exactly vertical. The cylinder is released to fall under gravity. Find the tension along the strings.
View Solution

